题目内容
[2014·浙江模拟]已知x0是函数f(x)＝2x＋
的一个零点．若x1∈(1，x0)，x2∈(x0，＋∞)，则( )
的一个零点．若x1∈(1，x0)，x2∈(x0，＋∞)，则( )| A．f(x1)＜0，f(x2)＜0 |
| B．f(x1)＜0，f(x2)＞0 |
| C．f(x1)＞0，f(x2)＜0 |
| D．f(x1)＞0，f(x2)＞0 |
B
构造函数y＝2x和函数y＝
，并画出函数的图象，可根据函数的图象进行判断．
在同一平面直角坐标系中画出函数y＝2x和函数y＝的图象，如图所示．
由图可知函数y＝2x和函数y＝的图象只有一个交点，即函数f(x)＝2x＋只有一个零点x0，且x0＞1.
因为x1∈(1，x0)，x2∈(x0，＋∞)，则由函数图象可知，f(x1)＜0，f(x2)＞0.
，并画出函数的图象，可根据函数的图象进行判断．在同一平面直角坐标系中画出函数y＝2x和函数y＝
的图象，如图所示．由图可知函数y＝2x和函数y＝
的图象只有一个交点，即函数f(x)＝2x＋只有一个零点x0，且x0＞1.因为x1∈(1，x0)，x2∈(x0，＋∞)，则由函数图象可知，f(x1)＜0，f(x2)＞0.
练习册系列答案
名校课堂系列答案
相关题目
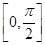上恒成立．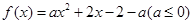
，
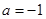，求函数的零点；
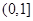上恰有一个零点，求
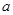的取值范围．
的方程
有实根，则实数
的取值范围为________．
所有零点之和等于 （ ）.
中，角
所对的边分别为
、
、
,若
的两根，且
;
的大小；
的长度；
的面积。