题目内容
某旅游公司提供甲、乙、丙三处旅游景点,游客选择游玩哪个景点互不影响,已知某游客选择游甲地而不选择游乙地和丙地的概率为0.08,选择游甲地和乙地而不选择游丙地的概率为0.12,在甲、乙、丙三处旅游景点中至少选择游一个景点0.88,用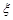 表示游客在甲、乙、丙三处旅游景点中选择游玩的景点数和没有选择游玩的景点数的乘积.
表示游客在甲、乙、丙三处旅游景点中选择游玩的景点数和没有选择游玩的景点数的乘积.
(Ⅰ)记“函数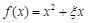 是R上的偶函数”为事件A,求事件A的概率;
是R上的偶函数”为事件A,求事件A的概率;
(Ⅱ)求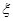 的概率分布列及数学期望.
的概率分布列及数学期望.
(Ⅰ)0.24;
(Ⅱ)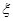 的概率分布列为:
的概率分布列为:
其数学期望是: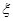
0 2 P 0.24 0.76 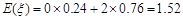
解析试题分析:根据独立事件的概率公式分别求出游客选择游玩甲、乙、丙景点的概率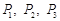 ,分别求出求事件A的概率和
,分别求出求事件A的概率和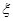 的概率分布列及数学期望.
的概率分布列及数学期望.
试题解析:
解:设该游客选择游玩甲、乙、丙景点的概率依次为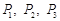 ,由题意知
,由题意知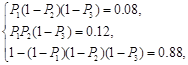 解得
解得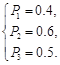 (3分)
(3分)
(Ⅰ)依题意,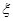 的所有可能取值为0,2.
的所有可能取值为0,2.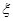 =0的意义是:该游客游玩的旅游景点数为3,没游玩的旅游景点数为0;或游玩的旅游景点数为0,没游玩的旅游景点数为3,
=0的意义是:该游客游玩的旅游景点数为3,没游玩的旅游景点数为0;或游玩的旅游景点数为0,没游玩的旅游景点数为3,
故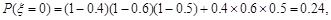 (6分)
(6分)
而函数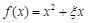 是R上的偶函数时
是R上的偶函数时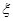 =0,
=0,
所以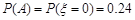 . (8分)
. (8分)
(Ⅱ)由(Ⅰ)知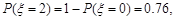 (10分)
(10分)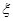 的概率分布列为:
的概率分布列为:
其数学期望是: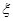
0 2 P 0.24 0.76 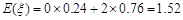 . (12分)
. (12分)
考点:独立事件的概率

 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案在一次联考后,某校对甲、乙两个文科班的数学考试成绩进行分析,规定:大于或等于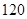 分为优秀,
分为优秀,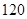 分以下为非优秀,统计成绩后,得到如下的
分以下为非优秀,统计成绩后,得到如下的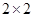 列联表,且已知在甲、乙两个文科班全部
列联表,且已知在甲、乙两个文科班全部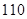 人中随机抽取人为优秀的概率为
人中随机抽取人为优秀的概率为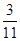 .
.
| | 优秀 | 非优秀 | 合计 |
| 甲班 | 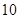 | | |
| 乙班 | | 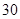 | |
| 合计 | | |  |
(2)根据列联表的数据,能否有
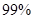 的把握认为成绩与班级有关系?
的把握认为成绩与班级有关系?(3)在甲、乙两个理科班优秀的学生中随机抽取两名学生,用
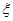 表示抽得甲班的学生人数,求
表示抽得甲班的学生人数,求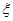 的分布列.
的分布列. 一个袋子中装有6个红球和4个白球,假设每一个球被摸到的可能性是相等的.
(Ⅰ)从袋子中摸出3个球,求摸出的球为2个红球和1个白球的概率;
(Ⅱ)从袋子中摸出两个球,其中白球的个数为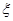 ,求
,求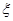 的分布列和数学期望.
的分布列和数学期望.
某超市为了解顾客的购物量及结算时间等信息,安排一名员工随机收集了在该超市购物的50位顾客的相关数据,如下表所示:
一次购物量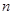 (件) (件) | 1≤n≤3 | 4≤n≤6 | 7≤n≤9 | 10≤n≤12 | n≥13 |
| 顾客数(人) |  | 20 | 10 | 5 | 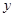 |
| 结算时间(分钟/人) | 0.5 | 1 | 1.5 | 2 | 2.5 |
(1)确定
 与
与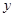 的值;
的值;(2)若将频率视为概率,求顾客一次购物的结算时间
 的分布列与数学期望;
的分布列与数学期望;(3)在(2)的条件下,若某顾客到达收银台时前面恰有2位顾客需结算,且各顾客的结算相互独立,求该顾客结算前的等候时间不超过2分钟的概率.
某高校在2013年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩共分五组,得到频率分布表如下表所示。
| 组号 | 分组 | 频数 | 频率 |
| 第一组 | [160,165) | 5 | 0.05 |
| 第二组 | [165,170) | 35 | 0.35 |
| 第三组 | [170,175) | 30 | a |
| 第四组 | [175,180) | b | 0.2 |
| 第五组 | [180,185) | 10 | 0.1 |
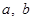 的值;
的值; (Ⅱ)为了能选出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样的方法抽取12人进入第二轮面试,求第3、4、5组中每组各抽取多少人进入第二轮的面试;考生李翔的笔试成绩为178分,但不幸没入选这100人中,那这样的筛选方法对该生而言公平吗?为什么?
(Ⅲ)在(2)的前提下,学校决定在12人中随机抽取3人接受“王教授”的面试,设第4组中被抽取参加“王教授”面试的人数为
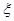 ,求
,求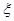 的分布列和数学期望.
的分布列和数学期望. 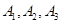 通晓日语,
通晓日语,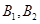 通晓俄语,
通晓俄语,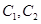 通晓韩语,从中选出通晓日语、俄语和韩语的志愿者各1名,组成一个小组.
通晓韩语,从中选出通晓日语、俄语和韩语的志愿者各1名,组成一个小组.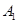 被选中的概率;(5分);(2)求
被选中的概率;(5分);(2)求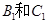 不全被选中的概率.(5分)
不全被选中的概率.(5分)

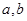 的值及分数在
的值及分数在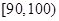 范围内的学生数,并估计这次考试全校学生数学成绩及格率(分数在
范围内的学生数,并估计这次考试全校学生数学成绩及格率(分数在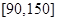 范围为及格);
范围为及格);