题目内容

9．命题“?x∈R，lgx=x-2”的否定是?x∈R，lgx≠x-2．

分析 利用特称命题的否定是全称命题写出结果即可．

解答 解：因为特称命题的否定是全称命题，所以命题“?x∈R，lgx=x-2”的否定是：?x∈R，lgx≠x-2．
故答案为：?x∈R，lgx≠x-2．

点评 本题考查命题的否定，特称命题与全称命题的否定关系，考查计算能力．

练习册系列答案
相关题目
19．已知数列{an}，其通项公式an=3n-18，则其前n项和Sn取最小值时n的值为（　　）
A．4B．5或6C．6D．5
20．已知函数f（x）=x-|x-1|，$g（x）={（\frac{1}{2}）^{x-1}}$．
（Ⅰ） 在所给坐标系中同时画出函数y=f（x）和y=g（x）的图象；
（Ⅱ） 根据（I）中图象写出不等式g（x）≥f（x）的解集．
17．已知集合M={-1，0，1，2，3，4}，N={-1，2，3，5}，P=M∩N，则P的子集共有（　　）
A．8个B．6个C．4个D．2个
4．已知函数$f（x）=a+\frac{2}{{{2^x}-1}}$（a∈R）；
（1）求函数f（x）的定义域；
（2）判断函数f（x）在区间（0，+∞）的单调性，用定义给出证明；
（3）是否存在实数a使函数f（x）为奇函数，若存在求出a，不存在说明理由．
14．函数y=3x+log3（x+1）在区间[0，2]上的值域为[1，10]．
1．已知函数f（x）=$\frac{ax+b}{{{x^2}+1}}$（x∈R，a、b为实数），且曲线y=f（x）在点$P（\frac{1}{3}，f（\frac{1}{3}））$处的切线l的方程是9x+10y-33=0．
（1）求实数a，b的值；
（2）现将切线方程改写为y=$\frac{3}{10}$（11-3x），并记g（x）=$\frac{3}{10}$（11-3x），当x∈[0，2]时，试比较f（x）与g（x）的大小关系．
18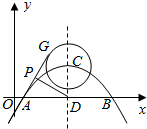．已知抛物线$y=-\frac{3}{16}（x-1）（x-9）$与x轴交于A，B两点，对称轴与抛物线交于点C，与x轴交于点D，⊙C的半径为2，G为⊙C上一动点，P为AG的中点，则DP的最大值为（　　）
A．$\frac{7}{2}$B．$\frac{{\sqrt{41}}}{2}$C．$\frac{{\sqrt{34}}}{2}$D．$2\sqrt{3}$
19．设向量$\overrightarrow{a}$=（1，2），$\overrightarrow{b}$=（2，3），若向量$\overrightarrow{a}$-λ$\overrightarrow{b}$与向量$\overrightarrow{c}$=（-5，-6）共线，则λ的值为$\frac{4}{3}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网