题目内容
(理科)若锐角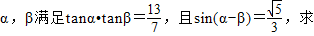
(1)cos(α-β); (2)cos(α+β)
【答案】分析:(1)由α,β为锐角,得到α-β的范围,再根据sin(α-β)的值大于0,得到α-β为锐角,故利用同角三角函数间的基本关系即可求出cos(α-β)的值;
(2)分别利用两角和与差的余弦函数公式化简 后,分子分母同时除以cosαcosβ,利用同角三角函数间的基本关系弦化切后,将tanαtanβ的值代入求出
后,分子分母同时除以cosαcosβ,利用同角三角函数间的基本关系弦化切后,将tanαtanβ的值代入求出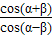 的值,然后再由(1)得到的cos(α-β)的值,即可求出cos(α+β)的值.
的值,然后再由(1)得到的cos(α-β)的值,即可求出cos(α+β)的值.
解答:解:(1)∵α,β为锐角,则-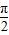 <α-β<
<α-β<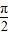 ,
,
而sin(α-β)= >0,则0<α-β<
>0,则0<α-β<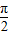 ,
,
∴cos(α-β)= =
= ;(6分)
;(6分)
(2)∵tanαtanβ=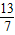 ,
,
∴ =
=
= =
=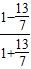 =-
=- ,
,
又cos(α-β)= ,
,
∴cos(α+β)=- .(12分)
.(12分)
点评:此题考查了同角三角函数间的基本关系,以及两角和与差的余弦函数公式,第二问先求出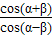 的值,然后借助第一问求出的cos(α-β)的值,从而得到cos(α+β)的值,注意此方法的技巧性.
的值,然后借助第一问求出的cos(α-β)的值,从而得到cos(α+β)的值,注意此方法的技巧性.
(2)分别利用两角和与差的余弦函数公式化简
 后,分子分母同时除以cosαcosβ,利用同角三角函数间的基本关系弦化切后,将tanαtanβ的值代入求出
后,分子分母同时除以cosαcosβ,利用同角三角函数间的基本关系弦化切后,将tanαtanβ的值代入求出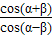 的值,然后再由(1)得到的cos(α-β)的值,即可求出cos(α+β)的值.
的值,然后再由(1)得到的cos(α-β)的值,即可求出cos(α+β)的值.解答:解:(1)∵α,β为锐角,则-
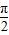 <α-β<
<α-β<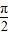 ,
,而sin(α-β)=
 >0,则0<α-β<
>0,则0<α-β<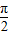 ,
,∴cos(α-β)=
 =
= ;(6分)
;(6分)(2)∵tanαtanβ=
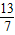 ,
,∴
 =
=
=
 =
=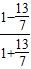 =-
=- ,
,又cos(α-β)=
 ,
,∴cos(α+β)=-
 .(12分)
.(12分)点评:此题考查了同角三角函数间的基本关系,以及两角和与差的余弦函数公式,第二问先求出
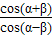 的值,然后借助第一问求出的cos(α-β)的值,从而得到cos(α+β)的值,注意此方法的技巧性.
的值,然后借助第一问求出的cos(α-β)的值,从而得到cos(α+β)的值,注意此方法的技巧性. 
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

