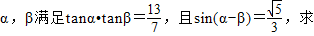Question

（理科）若锐角α，β满足tanα•tanβ=

13

7

，且sin(α-β)=

5

3

，求
（1）cos（α-β）； （2）cos（α+β）

Answer 1

（1）∵α，β为锐角，则-

π

2

＜α-β＜

π

2

，
而sin（α-β）=

5

3

＞0，则0＜α-β＜

π

2

，
∴cos（α-β）=

1-sin2(α-β)

=

2

3

；（6分）
（2）∵tanαtanβ=

13

7

，
∴

cos(α+β)

cos(α-β)

=

cosαcosβ-sinαsinβ

cosαcosβ+sinαsinβ

=

1-tanαtanβ

1+tanαtanβ

=

1- 13 7

1+ 13 7

=-

3

10

，
又cos（α-β）=

2

3

，
∴cos（α+β）=-

1

5

．（12分）