题目内容

已知平面上三个向量a、b、c的模均为1,它们相互之间的夹角为120°,求证:(a-b)⊥c.

证法一:∵|a|=|b|=|c|=1且a、b、c之间夹角均为120°,∴(a-b)·c=a·c-b·c=|a||c|cos120°-|b||c|cos120°=0.∴(a-b)⊥c.

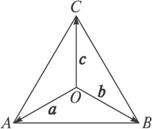
证法二:如图,设=a,=b,=c,

连结AB、AC、BC的三条线段围成正三角形ABC,O为△ABC的中心,

∴OC⊥AB.

又∵=a-b,∴(a-b)⊥c.

练习册系列答案
相关题目
已知平面上三个向量
a
，
b
，
c
的模均为1，它们相互之间的夹角均为120°．
（1）求证：(
a
-
b
)⊥
c
；
（2）若|k
a
+
b
+
c
|＞1 （k∈R），求k的取值范围．
已知平面上三个向量
a
 ，
b
 ，
c
，其中
a
=(1， 2)，
（1）若|
c
|=2
5
，且
a
∥
c
，求
c
的坐标；
（2）若|
b
|=
5
2
，且(
a
+2
b
)⊥(2
a
-
b
)，求
a
与
b
夹角的余弦值．
已知平面上三个向量
a
，
b
，
c
的模均为1，它们相互之间的夹角为120°，
（1）求证：(
b
-
c
)⊥
a
；
（2）若|t
a
+
b
+
c
|＞1（t∈R），求t的取值范围．
已知平面上三个向量|
a
|=|
b
|=|
c
|=2，它们之间的夹角都是120°．
（I）求
a
•
c
的值．
（II）求证：（
a
-
b
）⊥
c
．

已知平面上三个向量a、b、c的模均为1，它们相互之间的夹角均为120°.

(1)求证：（a-b）⊥c;

(2)若|ka+b+c|＞1 (k∈R)，求k的取值范围.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网