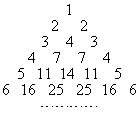
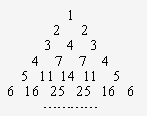
��Ŀ����
�����ò�����Ȼ���������µ���������aij(i��j)��ʾ��i�е�j����(i��jΪ������)��ʹail=aii=i ��ÿ���е���������ֱ�����䡰����ϵ�������֮��(��һ�����г��⣬��ͼ)�����n(nΪ������)���и���֮��Ϊbn��
��1����д��b2һ2b1����b3-2b2��b4-2b3,b5-2b4�����Ʋ�bn+1��bn�Ĺ�ϵ(����֤��)��
��2��֤������{bn+2}�ǵȱ����У���������{bn}��ͨ�ʽbn��
��3������{ bn}���Ƿ���ڲ�ͬ������bp��bq��br(p��q��rΪ������)ǡ�óɵȲ�����?���������P��q��r�Ĺ�ϵ���������ڣ���˵�����ɣ�
 |
��1��bn+1-2 bn=2��2��bn =3��2n-1-2��3��������
����:
��1��bl=1,��b2=4��b3=10��b4=22��b5=46��
�ɼ���b2-2 bl=2��b3-2 b2=2��b4-2 b3=2��b5-2 b4=2
�²⣺bn+1-2 bn=2 (��bn+1=2 bn+2��bn+1- bn=3��2n-1)
��2���ɣ�1�� ![]()
����{bn+2}������b1+2=3Ϊ���2Ϊ���ȵĵȱ����У�
�� bn+2=3��2n-1 ,��bn =3��2n-1-2����-
(ע�������ǣ�![]() �Ҳ�����n=1����1��)
�Ҳ�����n=1����1��)
��3��������{ bn }�д��ڲ�ͬ������bp, bq , br(p,q,r��N)ǡ�óɵȲ����У�������p>q>r,��Ȼ��{ bn }�ǵ������У���2 bq= bp, + br
��2����3��2q-1-2��=��3��2p-1-2��+��3��2r-1-2��,����2��2q-r=2q-r+1
��p,q,r��N��p>q>r֪��q-r��1��p-r��2
���ʽ�����Ϊż�����ұ�Ϊ��������������������{bn}�в����ڲ�ͬ������bp��bq��br(p,q,r��N)ǡ�óɵȲ�����--

 ��У����ϵ�д�
��У����ϵ�д�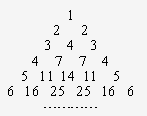 �����ò�����Ȼ���������µ���������aij��i��j����ʾ��i�е�j������i��jΪ����������ʹai1=aii=i��ÿ���е���������ֱ�����䡰����ϵ�������֮�ͣ���һ�����г��⣬��ͼ�������n��nΪ�����������и���֮��Ϊbn��
�����ò�����Ȼ���������µ���������aij��i��j����ʾ��i�е�j������i��jΪ����������ʹai1=aii=i��ÿ���е���������ֱ�����䡰����ϵ�������֮�ͣ���һ�����г��⣬��ͼ�������n��nΪ�����������и���֮��Ϊbn��