题目内容
已知直三棱柱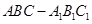 中,
中,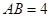 ,
,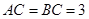 ,
,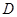 为
为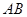 的中点。(Ⅰ)求异面直线
的中点。(Ⅰ)求异面直线 和
和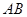 的距离;(Ⅱ)若
的距离;(Ⅱ)若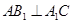 ,求二面角
,求二面角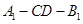 的平面角的余弦值。
的平面角的余弦值。

【答案】
:(Ⅰ) (Ⅱ)
(Ⅱ)
【解析】:(Ⅰ)如答(20)图1,因AC=BC,D为AB的中点,故CD  AB。又直三棱柱中,
AB。又直三棱柱中, 面
面 ,故
,故 ,所以异面直线
,所以异面直线 和AB的距离为
和AB的距离为
(Ⅱ):由 故
故 面
面 ,从而
,从而 ,
, 故
故 为所求的二面角
为所求的二面角 的平面角。
的平面角。
因 是
是 在面
在面 上的射影,又已知
上的射影,又已知 由三垂线定理的逆定理得
由三垂线定理的逆定理得 从而
从而 ,
, 都与
都与 互余,因此
互余,因此 ,所以
,所以 ≌
≌ ,因此
,因此 得
得
从而
所以在 中,由余弦定理得
中,由余弦定理得

练习册系列答案
相关题目
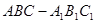 中,
中,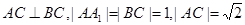 ,点M是
,点M是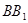 的中点,Q是AB的中点,
的中点,Q是AB的中点,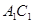 上的一动点,求证:
上的一动点,求证: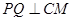 ;
;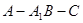 大小的余弦值.
大小的余弦值.
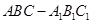 中,
中,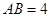 ,
,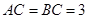 ,
,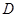 为
为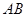 的中点。(Ⅰ)求点C到平面
的中点。(Ⅰ)求点C到平面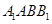 的距离;(Ⅱ)若
的距离;(Ⅱ)若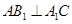 ,求二面角
,求二面角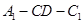 的平面角的余弦值。
的平面角的余弦值。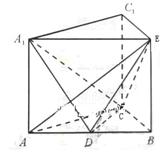
 中,△
中,△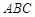 为等腰直角三角形,∠
为等腰直角三角形,∠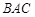 =90°,且
=90°,且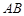 =
=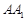 ,
,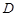 、
、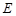 、
、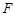 分别为
分别为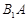 、
、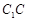 、
、 的中点.
的中点.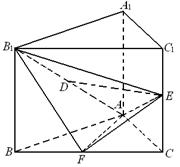
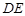 ∥平面
∥平面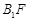 ⊥平面
⊥平面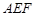 ;
;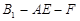 的余弦值
的余弦值 中,
中,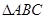 为等腰直角三角形,
为等腰直角三角形,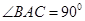 ,且
,且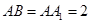 ,
, 分别为
分别为 的中点。
的中点。 //平面
//平面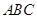 ;
;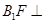 平面
平面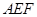 ;
;