题目内容
已知数列{an},{bn}中,对任何正整数n都有: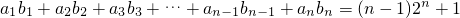 .
.
(1)若数列{bn}是首项为1和公比为2的等比数列,求数列{an}、{bn}的通项公式;
(2)若数列{an}是等差数列,数列{bn}是否为等比数列?若是,请求出通项公式,若不是,请说明理由.
解:(1)依题意,数列{bn}的通项公式为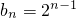 ,…(2分)
,…(2分)
由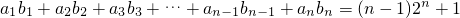 ,
,
可得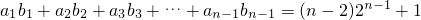 (n≥2),
(n≥2),
两式相减可得 ,即an=n.…(5分)
,即an=n.…(5分)
当n=1时,a1=1,从而对一切n∈N*,都有an=n.…(6分)
所以数列{an}的通项公式是an=n.…(7分)
(2)法1:设等差数列{an}的首项为a1,公差为d,则an=a1+(n-1)d.…(8分)
由(1)得, ,∴
,∴ (n≥2)
(n≥2)
∴ …(11分)
…(11分)
要使 是一个与n无关的常数,当且仅当a1=d≠0…(12分)
是一个与n无关的常数,当且仅当a1=d≠0…(12分)
即:当等差数列{an}的满足a1=d≠0时,数列{bn}是等比数列,其通项公式是 ;…(13分)
;…(13分)
当等差数列{an}的满足a1≠d时,数列{bn}不是等比数列. …(14分)
法2:设等差数列{an}的首项为a1,公差为d,则an=a1+(n-1)d.…(8分)
由(1)得, ,即
,即 (n≥2),若数列{bn}是等比数列,
(n≥2),若数列{bn}是等比数列,
则 …(11分)
…(11分)
要使上述比值是一个与n无关的常数,须且只需a1=d≠0.…(12分)
即:当等差数列{an}的满足a1=d≠0时,数列{bn}是等比数列,其通项公式是 ,…(13分)
,…(13分)
当等差数列{an}的满足a1≠d时,数列{bn}不是等比数列. …(14分)
分析:(1)确定数列{bn}的通项,利用再写一式,两式相减的方法,可求数列{an}的通项公式;
(2)确定bn的表达式,利用要使 是一个与n无关的常数,当且仅当a1=d≠0,即可得到结论.
是一个与n无关的常数,当且仅当a1=d≠0,即可得到结论.
点评:本题考查数列的通项,考查等比数列的确定,考查学生的计算能力,属于中档题.
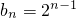 ,…(2分)
,…(2分)由
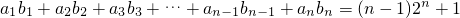 ,
,可得
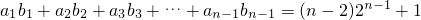 (n≥2),
(n≥2),两式相减可得
 ,即an=n.…(5分)
,即an=n.…(5分)当n=1时,a1=1,从而对一切n∈N*,都有an=n.…(6分)
所以数列{an}的通项公式是an=n.…(7分)
(2)法1:设等差数列{an}的首项为a1,公差为d,则an=a1+(n-1)d.…(8分)
由(1)得,
 ,∴
,∴ (n≥2)
(n≥2)∴
 …(11分)
…(11分) 要使
 是一个与n无关的常数,当且仅当a1=d≠0…(12分)
是一个与n无关的常数,当且仅当a1=d≠0…(12分)即:当等差数列{an}的满足a1=d≠0时,数列{bn}是等比数列,其通项公式是
 ;…(13分)
;…(13分)当等差数列{an}的满足a1≠d时,数列{bn}不是等比数列. …(14分)
法2:设等差数列{an}的首项为a1,公差为d,则an=a1+(n-1)d.…(8分)
由(1)得,
 ,即
,即 (n≥2),若数列{bn}是等比数列,
(n≥2),若数列{bn}是等比数列,则
 …(11分)
…(11分)要使上述比值是一个与n无关的常数,须且只需a1=d≠0.…(12分)
即:当等差数列{an}的满足a1=d≠0时,数列{bn}是等比数列,其通项公式是
 ,…(13分)
,…(13分)当等差数列{an}的满足a1≠d时,数列{bn}不是等比数列. …(14分)
分析:(1)确定数列{bn}的通项,利用再写一式,两式相减的方法,可求数列{an}的通项公式;
(2)确定bn的表达式,利用要使
 是一个与n无关的常数,当且仅当a1=d≠0,即可得到结论.
是一个与n无关的常数,当且仅当a1=d≠0,即可得到结论.点评:本题考查数列的通项,考查等比数列的确定,考查学生的计算能力,属于中档题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目