题目内容
已知集合D={(x1,x2)|x1>0,x2>0,x1+x2=k}(其中k为正常数).
(1)设u=x1x2,求u的取值范围;
(2)求证:当k≥1时不等式(
-x1)(
-x2)≤(
-
)2对任意(x1,x2)∈D恒成立;
(3)求使不等式(
-x1)(
-x2)≥(
-
)2对任意(x1,x2)∈D恒成立的k2的范围.
(1)设u=x1x2,求u的取值范围;
(2)求证:当k≥1时不等式(
| 1 |
| x1 |
| 1 |
| x2 |
| k |
| 2 |
| 2 |
| k |
(3)求使不等式(
| 1 |
| x1 |
| 1 |
| x2 |
| k |
| 2 |
| 2 |
| k |
(1)x1x2≤(
)2=
,当且仅当x1=x2=
时等号成立,
故u的取值范围为(0,
].
(2)解法一(函数法)(
-x1)(
-x2)=
+x1x2-
-
=x1x2+
-
=x1x2-
+2=u-
+2
由0<u≤
,又k≥1,k2-1≥0,
∴在(0,
]上是增函数
所以(
-x1)(
-x2)
=u-
+2≤
-
+2=
-2+
=(
-
)2
即当k≥1时不等式(
-x1)(
-x2)≤(
-
)2成立.
解法二(不等式证明的作差比较法)
(
-x1)(
-x2)-(
-
)2
=
+x1x2-
-
-
-
+2
=
-
-(
-x1x2)-(
+
-2)
=
-
-
,
将k2-4x1x2=(x1-x2)2代入得:
(
-x1)(
-x2)-(
-
)2
=
∵(x1-x2)2≥0,k≥1时4-k2x1x2-4k2=4(1-k2)-k2x1x2<0,
∴
≤0,
即当k≥1时不等式(
-x1)(
-x2)≤(
-
)2成立.
(3)解法一(函数法)
记(
-x1)(
-x2)=u+
+2=f(u),
则(
-
)2=f(
),
即求使f(u)≥f(
)对u∈(0,
]恒成立的k的范围.
由(2)知,要使(
-x1)(
-x2)≥(
-
)2
对任意(x1,x2)∈D恒成立,必有0<k<1,
因此1-k2>0,
∴函数f(u)=u+
+2在(0,
]上递减,在[
,+∞)上递增,
要使函数f(u)在(0,
]上恒有f(u)≥f(
),必有
≤
,即k4+16k2-16≤0,
解得0<k2≤4
-8.
解法二(不等式证明的作差比较法)
由(2)可知(
-x1)(
-x2)-(
-
)2=
,
要不等式恒成立,必须4-k2x1x2-4k2≥0恒成立
即x1x2≤
恒成立
由0<x1x2≤
得
≤
,即k4+16k2-16≤0,
解得0<k2≤4
-8.
因此不等式(
-x1)(
-x2)≥(
-
)2恒成立的k2的范围是0<k2≤4
-8
| x1+x2 |
| 2 |
| k2 |
| 4 |
| k |
| 2 |
故u的取值范围为(0,
| k2 |
| 4 |
(2)解法一(函数法)(
| 1 |
| x1 |
| 1 |
| x2 |
| 1 |
| x1x2 |
| x1 |
| x2 |
| x2 |
| x1 |
| 1 |
| x1x2 |
| ||||
| x1x2 |
| k2-1 |
| x1x2 |
| k2-1 |
| u |
由0<u≤
| k2 |
| 4 |
∴在(0,
| k2 |
| 4 |
所以(
| 1 |
| x1 |
| 1 |
| x2 |
=u-
| k2-1 |
| u |
| k2 |
| 4 |
| k2-1 | ||
|
| k2 |
| 4 |
| 4 |
| k2 |
| 2 |
| k |
| k |
| 2 |
即当k≥1时不等式(
| 1 |
| x1 |
| 1 |
| x2 |
| k |
| 2 |
| 2 |
| k |
解法二(不等式证明的作差比较法)
(
| 1 |
| x1 |
| 1 |
| x2 |
| k |
| 2 |
| 2 |
| k |
=
| 1 |
| x1x2 |
| x1 |
| x2 |
| x2 |
| x1 |
| 4 |
| k2 |
| k2 |
| 4 |
=
| 1 |
| x1x2 |
| 4 |
| k2 |
| k2 |
| 4 |
| x1 |
| x2 |
| x2 |
| x1 |
=
| k2-4x1x2 |
| k2x1x2 |
| k2-4x1x2 |
| 4 |
| (x1-x2)2 |
| x1x2 |
将k2-4x1x2=(x1-x2)2代入得:
(
| 1 |
| x1 |
| 1 |
| x2 |
| k |
| 2 |
| 2 |
| k |
=
| (x1-x2)2(4-k2x1x2-4k2) |
| 4k2x1x2 |
∵(x1-x2)2≥0,k≥1时4-k2x1x2-4k2=4(1-k2)-k2x1x2<0,
∴
| (x1-x2)2(4-k2x1x2-4k2) |
| 4k2x1x2 |
即当k≥1时不等式(
| 1 |
| x1 |
| 1 |
| x2 |
| k |
| 2 |
| 2 |
| k |
(3)解法一(函数法)
记(
| 1 |
| x1 |
| 1 |
| x2 |
| 1-k2 |
| u |
则(
| k |
| 2 |
| 2 |
| k |
| k2 |
| 2 |
即求使f(u)≥f(
| k2 |
| 4 |
| k2 |
| 4 |
由(2)知,要使(
| 1 |
| x1 |
| 1 |
| x2 |
| k |
| 2 |
| 2 |
| k |
对任意(x1,x2)∈D恒成立,必有0<k<1,
因此1-k2>0,
∴函数f(u)=u+
| 1-k2 |
| u |
| 1-k2 |
| 1-k2 |
要使函数f(u)在(0,
| k2 |
| 4 |
| k2 |
| 4 |
| k2 |
| 4 |
| 1-k2 |
解得0<k2≤4
| 5 |
解法二(不等式证明的作差比较法)
由(2)可知(
| 1 |
| x1 |
| 1 |
| x2 |
| k |
| 2 |
| 2 |
| k |
| (x1-x2)2(4-k2x1x2-4k2) |
| 4k2x1x2 |
要不等式恒成立,必须4-k2x1x2-4k2≥0恒成立
即x1x2≤
| 4-4k2 |
| k2 |
由0<x1x2≤
| k2 |
| 4 |
| k2 |
| 4 |
| 4-4k2 |
| k2 |
解得0<k2≤4
| 5 |
因此不等式(
| 1 |
| x1 |
| 1 |
| x2 |
| k |
| 2 |
| 2 |
| k |
| 5 |

练习册系列答案
相关题目

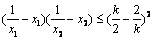 对任意(x1,x2) ∈D恒成立;
对任意(x1,x2) ∈D恒成立;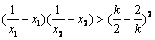 对任意(x1,x2) ∈D恒成立的k的范围.
对任意(x1,x2) ∈D恒成立的k的范围.