题目内容
 .
.
(1)当 时,求f(x)的值域;
时,求f(x)的值域;
(2)作出y=f(x)在长度为一个周期的闭区间上的简图;
(3)说明f(x)的图象可由y=sinx的图象经过怎样的变化得到?
解:(1) =
=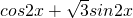 =
=
∵ ∴
∴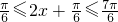 ,
,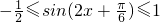
∴所求值域为[-1,2]
(2)列表

描点连线

(3)可由y=sinx的图象先向左平移 个单位,再将图象上各点的横坐标缩短到原来的
个单位,再将图象上各点的横坐标缩短到原来的 倍,纵坐标不变而得到.
倍,纵坐标不变而得到.
分析:先根据两角和与差公式对函数进行化简整理得f(x)=2sin(2x+ ),
),
(1)将2x+ 看作整体,求出取值范围,再根据正弦函数的性质求得函数的值域.
看作整体,求出取值范围,再根据正弦函数的性质求得函数的值域.
(2)令2x+ =0,
=0, ,求出x及对应的y值,描点连线.
,求出x及对应的y值,描点连线.
(3)先进行左移 个单位,再各点的横坐标缩短到原来的
个单位,再各点的横坐标缩短到原来的 倍.
倍.
点评:本题考查两角和与差公式、正弦函数的图象、性质、三角函数图象变换,考查转化、计算等能力.
 =
=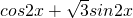 =
=
∵
 ∴
∴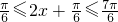 ,
,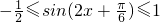
∴所求值域为[-1,2]
(2)列表

描点连线

(3)可由y=sinx的图象先向左平移
 个单位,再将图象上各点的横坐标缩短到原来的
个单位,再将图象上各点的横坐标缩短到原来的 倍,纵坐标不变而得到.
倍,纵坐标不变而得到.分析:先根据两角和与差公式对函数进行化简整理得f(x)=2sin(2x+
 ),
),(1)将2x+
 看作整体,求出取值范围,再根据正弦函数的性质求得函数的值域.
看作整体,求出取值范围,再根据正弦函数的性质求得函数的值域.(2)令2x+
 =0,
=0, ,求出x及对应的y值,描点连线.
,求出x及对应的y值,描点连线.(3)先进行左移
 个单位,再各点的横坐标缩短到原来的
个单位,再各点的横坐标缩短到原来的 倍.
倍.点评:本题考查两角和与差公式、正弦函数的图象、性质、三角函数图象变换,考查转化、计算等能力.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
 .
. 时,求f(x)的值域;
时,求f(x)的值域;
 时,求f(x)的最大值和最小值;
时,求f(x)的最大值和最小值; 上是单调增函数,且θ∈[0,2π),求θ的取值范围.
上是单调增函数,且θ∈[0,2π),求θ的取值范围.
 时,求f(x)的最大值和最小值;
时,求f(x)的最大值和最小值; 上是单调增函数,且θ∈[0,2π),求θ的取值范围.
上是单调增函数,且θ∈[0,2π),求θ的取值范围.
 时,求f(x)的最大值和最小值;
时,求f(x)的最大值和最小值; 上是单调增函数,且θ∈[0,2π),求θ的取值范围.
上是单调增函数,且θ∈[0,2π),求θ的取值范围.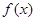 是定义在
是定义在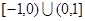 上的偶函数,当
上的偶函数,当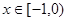 时,
时,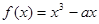 (
(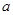 是实数)。
是实数)。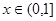 时,求f(x)的解析式;
时,求f(x)的解析式;