题目内容
如图,AC为圆O的直径,AP⊥圆O,PA=AB=BC.
(1)证明:面PAB⊥面PBC;
(2)若M、N分别为线段PB、PC的中点,试求直线PC与平面AMN所成角的正弦值.
(1)证明:面PAB⊥面PBC;
(2)若M、N分别为线段PB、PC的中点,试求直线PC与平面AMN所成角的正弦值.


(1)由题意,PA⊥面ABC,
∴PA⊥BC,又BC⊥AB,PA∩AB=A,
∴BC⊥面PAB
又BC?面PBC,
∴面PAB⊥面PBC
(2)∵BC⊥AB,BC⊥PA,AB∩PA=A
∴BC⊥平面PAB,又PB?平面PAB
∴BC⊥PB,又MN∥BC,∴MN⊥PB
在Rt△PAB中,PA=AB,M为中点,
∴AM⊥PB
∴AM∩MN=M,∴PB⊥面AMN
∴∠PNM即为所求角或其补角
设PA=2,则PB=2
| 2 |
| 2 |
| 2 |
| 3 |
| 3 |
∴sin∠PNM=
| PM |
| PN |
| ||
| 3 |
| ||
| 3 |

练习册系列答案
相关题目
 如图,某城市设立以城中心O为圆心、r公里为半径的圆形保护区,从保护区边缘起,在城中心O正东方向上有一条高速公路PB、西南方向上有一条一级公路QC,现要在保护区边缘PQ弧上选择一点A作为出口,建一条连接两条公路且与圆O相切的直道BC.已知通往一级公路的道路AC每公里造价为a万元,通往高速公路的道路AB每公里造价是m2a万元,其中a,r,m为常数,设∠POA=θ,总造价为y万元.
如图,某城市设立以城中心O为圆心、r公里为半径的圆形保护区,从保护区边缘起,在城中心O正东方向上有一条高速公路PB、西南方向上有一条一级公路QC,现要在保护区边缘PQ弧上选择一点A作为出口,建一条连接两条公路且与圆O相切的直道BC.已知通往一级公路的道路AC每公里造价为a万元,通往高速公路的道路AB每公里造价是m2a万元,其中a,r,m为常数,设∠POA=θ,总造价为y万元.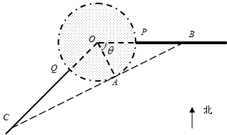 如图,某城市设立以城中心O为圆心、r公里为半径的圆形保护区,从保护区边缘起,在城中心O正东方向上有一条高速公路PB、西南方向上有一条一级公路QC,现要在保护区边缘PQ弧上选择一点A作为出口,建一条连接两条公路且与圆O相切的直道BC.已知通往一级公路的道路AC每公里造价为a万元,通往高速公路的道路AB每公里造价是m2a万元,其中a,r,m为常数,设∠POA=θ,总造价为y万元.
如图,某城市设立以城中心O为圆心、r公里为半径的圆形保护区,从保护区边缘起,在城中心O正东方向上有一条高速公路PB、西南方向上有一条一级公路QC,现要在保护区边缘PQ弧上选择一点A作为出口,建一条连接两条公路且与圆O相切的直道BC.已知通往一级公路的道路AC每公里造价为a万元,通往高速公路的道路AB每公里造价是m2a万元,其中a,r,m为常数,设∠POA=θ,总造价为y万元.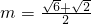 时,如何确定A点的位置才能使得总造价最低?
时,如何确定A点的位置才能使得总造价最低?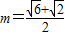 时,如何确定A点的位置才能使得总造价最低?
时,如何确定A点的位置才能使得总造价最低?
 与直线
与直线 的夹角大小为
的夹角大小为
 B.(不等式选讲)要使关于x的不等式
B.(不等式选讲)要使关于x的不等式 在实数
在实数