题目内容
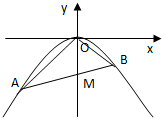 如图,抛物线y=-
如图,抛物线y=-| 1 |
| 2 |
| OA |
| OB |
| OM |
(1)求证:
| AM |
| AB |
(2)若
| MA |
| MB |
分析:(1)先确定x1x2=-4,再用坐标表示向量,利用向量共线的条件,即可得到结论;
(2)利用向量条件,确定A的坐标,再利用两点式,即可求AB所在直线方程.
(2)利用向量条件,确定A的坐标,再利用两点式,即可求AB所在直线方程.
解答:(1)证明:∵A(x1,y1)、B(x2,y2),且
•
=0,
∴x1x2+y1y2=0
∴x1x2+
(x1x2)2=0
∴x1x2=-4
∵
=(-x1,-2-y1)=(-x1,-2+
x12),
=(x2-x1,y2-y1)=(x2-x1,-
x12+
x22)
∴(-x1)(-
x12+
x22)+(x2-x1)(-2+
x12)=0
∴
∥
;
(2)解:∵
=-2
,∴(x1,2-
x12)=-2(x2,2-
x22)
∴x1=-2x2,
∵x1x2=-4,∴x2=
∴x1=-2x2=-2
∴y1=-
x12=-4,即A(-2
,-4)
∴AB所在直线方程为
=
,即y=
x-2.
| OA |
| OB |
∴x1x2+y1y2=0
∴x1x2+
| 1 |
| 4 |
∴x1x2=-4
∵
| AM |
| 1 |
| 2 |
| AB |
| 1 |
| 2 |
| 1 |
| 2 |
∴(-x1)(-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴
| AM |
| AB |
(2)解:∵
| MA |
| MB |
| 1 |
| 2 |
| 1 |
| 2 |
∴x1=-2x2,
∵x1x2=-4,∴x2=
| 2 |
∴x1=-2x2=-2
| 2 |
∴y1=-
| 1 |
| 2 |
| 2 |
∴AB所在直线方程为
| y+2 |
| -4+2 |
| x | ||
-2
|
| ||
| 2 |
点评:本题考查直线与抛物线的位置关系,考查向量知识的运用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
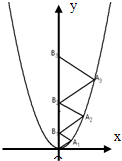 如图,抛物线y=x2第一象限部分上的一系列点Ai(i=1,2,3,…,n,…)与y正半轴上的点B1及原点,构成一系列正三角形AiBi-1Bi(记B0为O),记ai=|AiAi+1|.
如图,抛物线y=x2第一象限部分上的一系列点Ai(i=1,2,3,…,n,…)与y正半轴上的点B1及原点,构成一系列正三角形AiBi-1Bi(记B0为O),记ai=|AiAi+1|. 已知如图,抛物线y=ax2+bx+2与x轴的交点是A(3,0)、B(6,0),与y轴的交点是C.
已知如图,抛物线y=ax2+bx+2与x轴的交点是A(3,0)、B(6,0),与y轴的交点是C.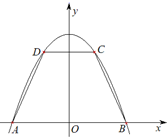 (2012•西城区一模)如图,抛物线y=-x2+9与x轴交于两点A,B,点C,D在抛物线上(点C在第一象限),CD∥AB.记|CD|=2x,梯形ABCD面积为S.
(2012•西城区一模)如图,抛物线y=-x2+9与x轴交于两点A,B,点C,D在抛物线上(点C在第一象限),CD∥AB.记|CD|=2x,梯形ABCD面积为S. 如图,抛物线y=ax2-5ax+4经过△ABC的三个顶点,已知BC∥x轴,点A在x轴上,点C在y轴上,且AC=BC.
如图,抛物线y=ax2-5ax+4经过△ABC的三个顶点,已知BC∥x轴,点A在x轴上,点C在y轴上,且AC=BC.