题目内容
 如图,抛物线y=ax2-5ax+4经过△ABC的三个顶点,已知BC∥x轴,点A在x轴上,点C在y轴上,且AC=BC.
如图,抛物线y=ax2-5ax+4经过△ABC的三个顶点,已知BC∥x轴,点A在x轴上,点C在y轴上,且AC=BC.(1)写出A,B,C三点的坐标并求抛物线的解析式;
(2)探究:若点P是抛物线对称轴上且在x轴下方的动点,是否存在△PAB是等腰三角形.若存在,求出所有符合条件的点P坐标;不存在,请说明理由.
分析:(1)在抛物线线y=ax2-5ax+4中,令x=0可得点C坐标,由BC∥x轴可得B和C关于对称轴对称对称,从而可求B,由点A在x轴上及AC=BC=5可求A,把点A坐标代入y=ax2-5ax+4中可求a,进而可求抛物线的方程
(2)分三类情形考虑:①以AB为腰且顶角为角A的△PAB有1个)②以AB为腰且顶角为角B的△PAB有1个③以AB为底,顶角为角P的△PAB有1个,即△P3AB.分别进行求解P的坐标
(2)分三类情形考虑:①以AB为腰且顶角为角A的△PAB有1个)②以AB为腰且顶角为角B的△PAB有1个③以AB为底,顶角为角P的△PAB有1个,即△P3AB.分别进行求解P的坐标
解答: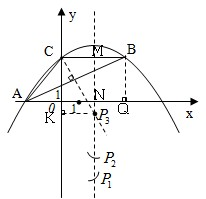 解:(1)在抛物线线y=ax2-5ax+4中,令x=0可得点C坐标为(0,4),抛物线的对称轴是x=
解:(1)在抛物线线y=ax2-5ax+4中,令x=0可得点C坐标为(0,4),抛物线的对称轴是x=
∵BC∥x轴
∴B和C关于直线x=
对称,从而有B(5,4)
∵点A在x轴上 AC=BC=5
∴A(-3,0)…(3分)
把点A坐标代入y=ax2-5ax+4中,解得a=-
∴y=-
x2+
x+4…(5分)
(2)存在符合条件的点P共有3个.以下分三类情形 探索.
设抛物线对称轴与x轴交于N,与CB交于M.
过点B作BQ⊥x轴于Q,易得BQ=4,AQ=8,AN=5.5,BM=
①以AB为腰且顶角为角A的△PAB有1个:△P1AB.∴AB2=AQ2+BQ2=82+42=80
在 Rt△ANP1中,P1N=
=
=
=
∴P1(
,-
)(7分)
②以AB为腰且顶角为角B的△PAB有1个:△P2AB.
在 Rt△BMP2中,MP2=
=
=
=
∴P2(
,
)(9分)
③以AB为底,顶角为角P的△PAB有1个,即△P3AB.
画AB的垂直平分线交抛物线对称轴于P3,此时平分线必过等腰△ABC的顶点C.
过点P3作P3K垂直y轴,垂足为K,显然 Rt△P3CK∽Rt△BAQ.∴
=
=
.∵P3K=2.5∴CK=5于是OK=1P3(
,-1)(11分)
所有符合条件的点P坐标为(
,-
),(
,
)、(
,-1)…(12分)
注:第(3)小题中,只写出点P的坐标,无任何说明者不得分.
 解:(1)在抛物线线y=ax2-5ax+4中,令x=0可得点C坐标为(0,4),抛物线的对称轴是x=
解:(1)在抛物线线y=ax2-5ax+4中,令x=0可得点C坐标为(0,4),抛物线的对称轴是x=| 5 |
| 2 |
∵BC∥x轴
∴B和C关于直线x=
| 5 |
| 2 |
∵点A在x轴上 AC=BC=5
∴A(-3,0)…(3分)
把点A坐标代入y=ax2-5ax+4中,解得a=-
| 1 |
| 6 |
∴y=-
| 1 |
| 6 |
| 5 |
| 6 |
(2)存在符合条件的点P共有3个.以下分三类情形 探索.
设抛物线对称轴与x轴交于N,与CB交于M.
过点B作BQ⊥x轴于Q,易得BQ=4,AQ=8,AN=5.5,BM=
| 5 |
| 2 |
①以AB为腰且顶角为角A的△PAB有1个:△P1AB.∴AB2=AQ2+BQ2=82+42=80
在 Rt△ANP1中,P1N=
A
|
| AB2-AN2 |
| 80-(5.5)2 |
| ||
| 2 |
| 5 |
| 2 |
| ||
| 2 |
②以AB为腰且顶角为角B的△PAB有1个:△P2AB.
在 Rt△BMP2中,MP2=
B
|
| AB2-BM2 |
80-
|
| ||
| 2 |
| 5 |
| 2 |
8-
| ||
| 2 |
③以AB为底,顶角为角P的△PAB有1个,即△P3AB.
画AB的垂直平分线交抛物线对称轴于P3,此时平分线必过等腰△ABC的顶点C.
过点P3作P3K垂直y轴,垂足为K,显然 Rt△P3CK∽Rt△BAQ.∴
| P3K |
| CK |
| BQ |
| AQ |
| 1 |
| 2 |
| 5 |
| 2 |
所有符合条件的点P坐标为(
| 5 |
| 2 |
| ||
| 2 |
| 5 |
| 2 |
8-
| ||
| 2 |
| 5 |
| 2 |
注:第(3)小题中,只写出点P的坐标,无任何说明者不得分.
点评:本题主要考查了由抛物线的性质求解抛物线的方程,及直线与抛物线位置关系的应用,解题(2)要求考生具备较强的逻辑推理与运算的能力.

练习册系列答案
相关题目
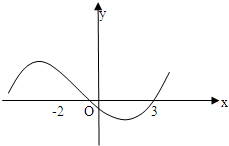 知函数f(x)=ax3+bx2+cx+d(a>0)图象如图,则
知函数f(x)=ax3+bx2+cx+d(a>0)图象如图,则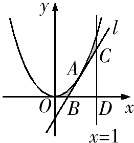 如图,抛物线y=x2上有一点A(a,a2),a∈(0,1),过点A引抛物线的切线l分别交x轴与直线x=1于B,C两点,直线x=1交x轴于点D.
如图,抛物线y=x2上有一点A(a,a2),a∈(0,1),过点A引抛物线的切线l分别交x轴与直线x=1于B,C两点,直线x=1交x轴于点D. 已知如图,抛物线y=ax2+bx+2与x轴的交点是A(3,0)、B(6,0),与y轴的交点是C.
已知如图,抛物线y=ax2+bx+2与x轴的交点是A(3,0)、B(6,0),与y轴的交点是C.