题目内容
如图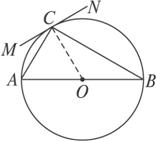
BC,则sin∠MCA等于( )
图
A.
B. 
C.
D. 
解析:连结OC,∵MN切圆于C,
∴OC⊥MN,即∠MCA+∠ACO=90°.
∵AB是直径,∴∠ACB=90°,
即∠ACO+∠OCB=90°.
∵OB=OC,∴∠B=∠OCB.
∴∠MCA=∠B.
又在Rt△ABC中,AB=
AC,
∴sinB==.
∴sin∠MCA=.
答案:D
练习册系列答案
阅读快车系列答案
相关题目
上一动点(点P不与A、C重合),连结PC、PD、PA、AD,点E在AP的延长线上,PD与AB交于点F.给出下列四个结论:①CH2=AH·BH;②
=
;③AD2=DF·DP;④∠EPC=∠APD.
=a，
=b，用a、b表示
=_____________.
=a，
=b，
=c，且|a|=2，|b|=1，|c|=3，试用a和b表示c. 