Question

已知两点A(-3,4)、B(3,2),过点P(2,-1)的直线l与线段AB有公共点.

(1)求直线l的斜率k的取值范围;

(2)求直线l的倾斜角θ的取值范围.

Answer 1

思路分析：画一个草图,结合图形考虑,为使l与线段AB有公共点,l的倾斜角应介于直线PB与直线PA的倾斜角之间,但由于l的倾斜角要“跨越”90°,所以要特别注意,当l的倾斜角小于90°时,有k≥k_PB;当l的倾斜角大于90°时,则有k≤k_PA.

解：如图,由题可知

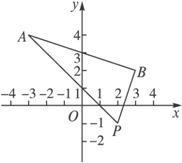
k_PA==-1,              k_PB==3.

    (1)要使l与线段AB有公共点,则直线l的斜率k的取值范围是k≤-1或k≥3.

    (2)由题可知直线l的倾斜角介于直线PB与PA的倾斜角之间.又PB的倾斜角是arctan3,PA的倾斜角是,

    ∴α的取值范围是{α|arctan3≤α≤}.