题目内容
已知函数
(1) 当 时,求函数
时,求函数 的最小值
的最小值 ;
;
(2) 是否存在实数 ,使得
,使得 的定义域为
的定义域为 ,值域为
,值域为 ,若存在,求出
,若存在,求出 、
、 的值;若不存在,则说明理由
的值;若不存在,则说明理由

(1) 当
 时,求函数
时,求函数 的最小值
的最小值 ;
;(2) 是否存在实数
 ,使得
,使得 的定义域为
的定义域为 ,值域为
,值域为 ,若存在,求出
,若存在,求出 、
、 的值;若不存在,则说明理由
的值;若不存在,则说明理由(1)

(2)满足题意的
 、
、 不存在
不存在(1) 设 ,∵
,∵ ,∴
,∴ ,
,
则


当 时,
时, ;当
;当 时,
时, ;
;
当 时,
时, .∴
.∴ .
.
(2) ∵ ,∴
,∴ ,在
,在 上是减函数.
上是减函数.
∵ 的定义域为
的定义域为 ,值域为
,值域为 , ∴
, ∴ ,
, 
②-①得: ,
,
∵ ,∴
,∴ .但这与“
.但这与“ ”矛盾. ∴满足题意的
”矛盾. ∴满足题意的 、
、 不存在
不存在
 ,∵
,∵ ,∴
,∴ ,
,则



当
 时,
时, ;当
;当 时,
时, ;
;当
 时,
时, .∴
.∴ .
.(2) ∵
 ,∴
,∴ ,在
,在 上是减函数.
上是减函数.∵
 的定义域为
的定义域为 ,值域为
,值域为 , ∴
, ∴ ,
, 
②-①得:
 ,
,∵
 ,∴
,∴ .但这与“
.但这与“ ”矛盾. ∴满足题意的
”矛盾. ∴满足题意的 、
、 不存在
不存在
练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
 的定义域为R,求实数m的取值范围
的定义域为R,求实数m的取值范围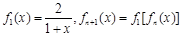 ,且
,且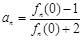 ,则
,则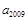 等于( )
等于( )
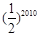
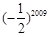
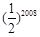
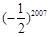
 ,
, 的定义域;
的定义域; 是否有根?如果有根
是否有根?如果有根 ,请求出一个长度为
,请求出一个长度为 的区间
的区间 , 使
, 使 ;如果没有,请说明理由?(注:区间
;如果没有,请说明理由?(注:区间 的长度
的长度 )
)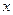

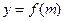
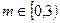



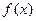 是定义在
是定义在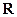 内、以
内、以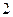 为周期的函数,当
为周期的函数,当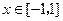 时,
时,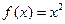 .
.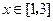 时,
时,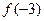 ,
,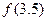 的值.
的值. 的定义域为[-1,2],那么函数
的定义域为[-1,2],那么函数 中的x的取值范围是( )
中的x的取值范围是( ) ]
]