题目内容
已知0＜α＜π，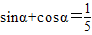
，求tanα的值．
【答案】分析：将已知等式平方并结合sin2α+cos2α=1，算出2sinαcosα=-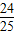
，由此算出（sinα-cosα）2=
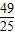，得sinα-cosα=
（舍负）从而解出sinα=
，cosα=-
，再利用同角三角函数的商数关系，即可算出tanα的值．
解答：解：∵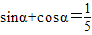
…①
∴平方得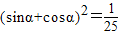
，即1+2sinαcosα=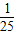
可得2sinαcosα=-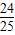
因此，（sinα-cosα）2=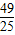
，得sinα-cosα=
（舍负），…②
①②联解，得sinα=
，cosα=-
∴tanα=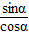
=-
点评：本题给出角α的正弦与余弦之和，求α的正切之值．着重考查了同角三角函数关系的知识，属于基础题．
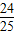，由此算出（sinα-cosα）2=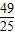，得sinα-cosα=（舍负）从而解出sinα=，cosα=-，再利用同角三角函数的商数关系，即可算出tanα的值．解答：解：∵
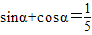…①∴平方得
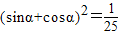，即1+2sinαcosα=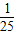可得2sinαcosα=-
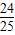
因此，（sinα-cosα）2=
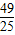，得sinα-cosα=（舍负），…②①②联解，得sinα=
，cosα=-∴tanα=
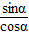=-点评：本题给出角α的正弦与余弦之和，求α的正切之值．着重考查了同角三角函数关系的知识，属于基础题．
练习册系列答案
名师指导一卷通系列答案
相关题目
，tan
+cot
，求sin(
)的值.
＜α＜
,cos(
-α)=
,sin(
+β)=
,求sin(α+β)的值.
为焦点的双曲线C：
（a＞0，b＞0）上的一点，已知
=0，
．
；
，
= 0，求双曲线的方程．