题目内容
如图,正方体ABCD—A1B(1)求证:AC1∥平面BED;
(2)求二面角A1BDE的大小.
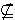
解法一:(1)方法一:证明:连结AC交BD于O,连结OE. ?
∵E为棱CC1的中点,?
又∵在正方形ABCD中,O是AC的中点,?
∴OE∥AC1. ?
又∵OE![]() 平面BED,AC1
平面BED,AC1![]() 平面BED,?
平面BED,?
∴AC1∥平面BED.
 ?
?
方法二:证明:∵![]() =
=![]() +
+![]() +
+![]() ??
??
=![]() +
+![]() +2
+2![]() ??
??
=(![]() +
+![]() )+(
)+(![]() +
+![]() )?
)?
=![]() +
+![]() , ?
, ?
又∵![]() 与
与![]() 不共线,∴
不共线,∴![]() 与
与![]() 、
、![]() 共面.?
共面.?
又∵AC1![]() 平面BED,∴AC1∥平面BED. ?
平面BED,∴AC1∥平面BED. ?
(2)解:连结A1O,A1E. ?
在等边△A1BD中,A1O⊥BD,?
∵△BEC≌△DEC,?
∴BE=DE.又∵O为BD中点,?
∴OE⊥BD.∴∠A1OE为二面角A1-BD-E的平面角. ?
在正方体ABCD—A1B
∵E为棱CC1的中点,由平面几何知识得?
EO=![]() a,A1O=
a,A1O=![]() a,A1E=
a,A1E=
方法一:∴cos∠A1OE=![]()
?
= =0.?
=0.?
∴∠A1OE=90°.?
故二面角A1-BD-E为90°. ?
方法二:∵A1E2=A1O2+EO2,∴∠A1OE=90°.?
故二面角A1-BD-E为90°. ?
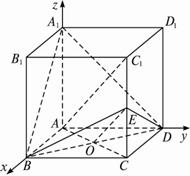
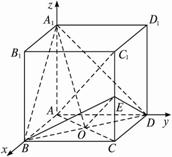
解法二:如图所示建立空间直角坐标系A-xyz, 设AD=
(1)方法一:A(0,0,0),C(
连结AC交BD于O,连结OE.?
∵O为AC中点,∴O(a,a,0).?
又E为CC1中点,∴E(
∴![]() =(
=(![]() =(a,a,a).?
=(a,a,a).?
∴![]() =2
=2![]() .∴
.∴![]() ∥
∥![]() . ?
. ?
又∵AC1与OE不共线,∴AC1∥OE.?
又OE![]() 平面BED,AC1
平面BED,AC1![]() 平面BED,?
平面BED,?
∴AC1∥平面BED.
 ?
?
方法二:![]() =(0,
=(0,![]() =(
=(![]() =(
=(
假设存在实数x、y,使![]() =x
=x![]() +y
+y![]() ,?
,?
则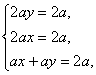 解得
解得![]()
∴![]() =
=![]() +
+![]() . ?
. ?
又∵![]() 与
与![]() 不共线.∴
不共线.∴![]() 与
与![]() 、
、![]() 共面.?
共面.?
又∵AC1![]() 平面BED,∴AC1∥平面BED. ?
平面BED,∴AC1∥平面BED. ?
(2)方法一:连结A1O,OE.在等边△A1BD中,A1O⊥BD.?
∵△BEC≌△DEC,?
∴BE=DE.?
又∵O为BD中点,?
∴OE⊥BD.∴∠A1OE为二面角A1-BD-E的平面角. ?
∵![]() =(-a,-a,
=(-a,-a,![]() =(a,a,a), ?
=(a,a,a), ?
∴cos〈![]() ,
,![]() 〉=
〉=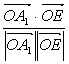 ?
?
=![]() =0.?
=0.?
∴〈![]() ,
,![]() 〉=90°.故二面角A1-BD-E为90°. ?
〉=90°.故二面角A1-BD-E为90°. ?
方法二:![]() =(
=(![]() =(0,
=(0,![]() =(
=(
设平面A1BD的法向量为n=(x,y,z),?
由n·![]() =0及n·
=0及n·![]() =0,得
=0,得![]() 取x=1,y=z=1,则n=(1,1,1). ?
取x=1,y=z=1,则n=(1,1,1). ?
设平面BED的法向量为m=(x,y,z),?
由m·![]() =0,m·
=0,m·![]() =0,得
=0,得![]() 取y=1,则x=1,z=-2.?
取y=1,则x=1,z=-2.?
∴m=(1,1,-2). ?
cos〈n,m〉=![]() =
=![]() =0.?
=0.?
∴〈n,m〉=90°.?
故二面角A1-BD-E为90°.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
 如图,正方体ABCD-A1B1C1D1中,E,F分别为BB1和A1D1的中点.证明:向量
如图,正方体ABCD-A1B1C1D1中,E,F分别为BB1和A1D1的中点.证明:向量 如图,正方体ABCD-A1B1C1D1棱长为8,E、F分别为AD1,CD1中点,G、H分别为棱DA,DC上动点,且EH⊥FG.
如图,正方体ABCD-A1B1C1D1棱长为8,E、F分别为AD1,CD1中点,G、H分别为棱DA,DC上动点,且EH⊥FG. 如图,正方体ABCD-A1B1C1D1中,若E、F、G分别为棱BC、C1C、B1C1的中点,O1、O2分别为四边形ADD1A1、A1B1C1D1的中心,则下列各组中的四个点不在同一个平面上的是( )
如图,正方体ABCD-A1B1C1D1中,若E、F、G分别为棱BC、C1C、B1C1的中点,O1、O2分别为四边形ADD1A1、A1B1C1D1的中心,则下列各组中的四个点不在同一个平面上的是( ) 如图,正方体ABCD-A1B1C1D1中,E、F、G、H分别是所在棱的三等分点,且
如图,正方体ABCD-A1B1C1D1中,E、F、G、H分别是所在棱的三等分点,且