题目内容
【题目】已知圆![]() ,点
,点![]() ,点
,点![]() 是圆上任意一点,线段
是圆上任意一点,线段![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,设动点
,设动点![]() 的轨迹为
的轨迹为![]() .
.
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)设直线![]() 与轨迹
与轨迹![]() 交于
交于![]() 两点,
两点, ![]() 为坐标原点,若
为坐标原点,若![]() 的重心恰好在圆
的重心恰好在圆![]() 上,求
上,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)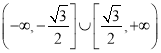 .
.
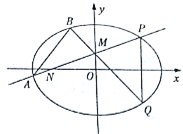
【解析】试题分析:(1)如图,通过|QP|=|QN|,|MQ|+|QN|=|MP|=4,可知点Q的轨迹是以M、N为焦点,长轴长等于4的椭圆,即得椭圆C的方程;(2)设点G(x1,y1),H(x2,y2),联立直线l与椭圆C的方程,由韦达定理得x1+x2,从而可得y1+y2,及△GOH的重心的坐标并将其代入圆的方程,通过计算得![]() <1+4k2(k≠0),利用不等式即得实数m的取值范围.
<1+4k2(k≠0),利用不等式即得实数m的取值范围.
解析:
(Ⅰ)如图, ![]()
![]()

故点![]() 的轨迹是以
的轨迹是以![]() 为焦点,长轴长等于4的椭圆
为焦点,长轴长等于4的椭圆
所以椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)设点![]()
方程联立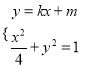 得,
得, ![]()
![]() ,
, ![]()
所以![]() 的重心的坐标为
的重心的坐标为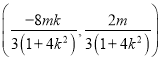
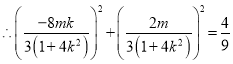
整理得: 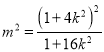 ①
①
![]()
依题意 ![]() 得
得 ![]() ②
②
由①、②易得 ![]()
设![]() ,则
,则![]()
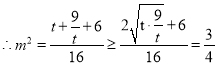 ,当且仅当
,当且仅当![]() 取等号
取等号
所以实数![]() 的取值范围是
的取值范围是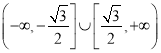 .
.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目