题目内容
设f(x)=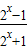 .
.(Ⅰ)判断f(x)的单调性,并加以证明;
(Ⅱ)求证对任意非零实数x,都有
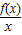 >0.
>0.
【答案】分析:(Ⅰ)由于 f(x)=1-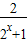 ,设x1<x2,计算 f(x1)-f(x2)=
,设x1<x2,计算 f(x1)-f(x2)=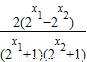 <0,即 f(x1)<f(x2),可得函数f(x)在R上是增函数.
<0,即 f(x1)<f(x2),可得函数f(x)在R上是增函数.
(Ⅱ)由于当x>0时,2x-1>0,f(x)=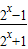 >0;当x<0时,2x-1<0,f(x)=
>0;当x<0时,2x-1<0,f(x)=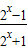 <0,命题得证.
<0,命题得证.
解答:解:(Ⅰ)由于 f(x)=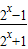 =1-
=1-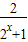 ,设x1<x2,
,设x1<x2,
∵f(x1)-f(x2)=(1-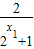 )-(1-
)-(1-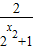 )=
)=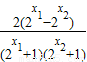 <0,即 f(x1)<f(x2),故函数f(x)在R上是增函数.
<0,即 f(x1)<f(x2),故函数f(x)在R上是增函数.
(Ⅱ)由于当x>0时,2x-1>0,f(x)=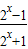 >0;当x<0时,2x-1<0,f(x)=
>0;当x<0时,2x-1<0,f(x)=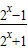 <0,
<0,
∴对任意非零实数x,都有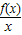 >0.
>0.
点评:本题主要考查函数的单调性的判断和证明,函数的单调性的性质应用,属于中档题.
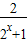 ,设x1<x2,计算 f(x1)-f(x2)=
,设x1<x2,计算 f(x1)-f(x2)=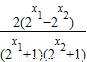 <0,即 f(x1)<f(x2),可得函数f(x)在R上是增函数.
<0,即 f(x1)<f(x2),可得函数f(x)在R上是增函数.(Ⅱ)由于当x>0时,2x-1>0,f(x)=
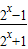 >0;当x<0时,2x-1<0,f(x)=
>0;当x<0时,2x-1<0,f(x)=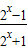 <0,命题得证.
<0,命题得证.解答:解:(Ⅰ)由于 f(x)=
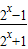 =1-
=1-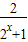 ,设x1<x2,
,设x1<x2,∵f(x1)-f(x2)=(1-
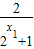 )-(1-
)-(1-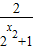 )=
)=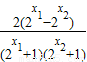 <0,即 f(x1)<f(x2),故函数f(x)在R上是增函数.
<0,即 f(x1)<f(x2),故函数f(x)在R上是增函数.(Ⅱ)由于当x>0时,2x-1>0,f(x)=
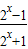 >0;当x<0时,2x-1<0,f(x)=
>0;当x<0时,2x-1<0,f(x)=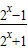 <0,
<0,∴对任意非零实数x,都有
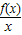 >0.
>0.点评:本题主要考查函数的单调性的判断和证明,函数的单调性的性质应用,属于中档题.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案
相关题目
设f(x)在[0,1]上有定义,要使函数f(x-a)+f(x+a)有定义,则a的取值范围为( )
A、(-∞,-
| ||||
B、[-
| ||||
C、(
| ||||
D、(-∞,-
|