题目内容
2.已知函数f(x)=sin(ωx+φ)+cos(ωx+φ)(ω>0,0<φ<π)是奇函数,直线y=$\sqrt{2}$与函数f(x)的图象的两个相邻交点的距离为$\frac{π}{2}$,则( )| A. | f(x)在(0,$\frac{π}{4}$)上单调递减 | B. | f(x)在($\frac{π}{8}$,$\frac{3π}{8}$)上单调递减 | ||
| C. | f(x)在(0,$\frac{π}{4}$)上单调递增 | D. | f(x)在($\frac{π}{8}$,$\frac{3π}{8}$)上单调递增 |
分析 利用辅助角化简函数f(x)=sin(ωx+φ)+cos(ωx+φ)=$\sqrt{2}$sin(ωx+φ$+\frac{π}{4}$)是奇函数,可得φ$+\frac{π}{4}$=kπ,解出φ,直线y=$\sqrt{2}$与函数f(x)的图象的两个相邻交点的距离为$\frac{π}{2}$,可得周期T=$\frac{π}{2}$,求出ω,可得f(x)的解析式,从而判断各选项即可.
解答 解:化简函数f(x)=sin(ωx+φ)+cos(ωx+φ)=$\sqrt{2}$sin(ωx+φ$+\frac{π}{4}$)
∵f(x)是奇函数,
∴φ$+\frac{π}{4}$=kπ,k∈Z.即φ=k$π-\frac{π}{4}$.
∵0<φ<π
∴φ=$\frac{3π}{4}$.
又∵直线y=$\sqrt{2}$与函数f(x)的图象的两个相邻交点的距离为$\frac{π}{2}$,
可得周期T=$\frac{π}{2}$,即$\frac{2π}{ω}=\frac{π}{2}$,
∴ω=4.
∴f(x)的解析式为f(x)=$\sqrt{2}$sin(4x+$\frac{3π}{4}$),
令2kπ$-\frac{π}{2}≤$4x+$\frac{3π}{4}$$≤\frac{π}{2}$+2kπ,单调递增.
可得:$\frac{1}{2}kπ$$-\frac{5π}{16}≤x≤-\frac{π}{16}$+$\frac{1}{2}kπ$,k∈Z.
∴C选项对.D选项不对.
令2kπ+$\frac{π}{2}$≤4x+$\frac{3π}{4}$$≤\frac{3π}{2}$+2kπ,单调递减.
可得:$\frac{1}{2}kπ$$-\frac{π}{16}≤x≤\frac{3π}{16}$$+\frac{1}{2}kπ$,k∈Z.
∴A,B选项不对.
故选C.
点评 本题主要考查三角函数的图象和性质,利用三角函数公式将函数进行化简是解决本题的关键.

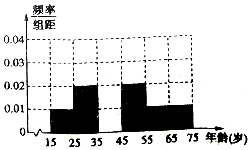 河南多地遭遇年霾,很多学校调整元旦放假时间,提前放假让学生们在家躲霾.郑州市根据《郑州市人民政府办公厅关于将重污染天气黄色预警升级为红色预警的通知》,自12月29日12时将黄色预警升级为红色预警,12月30日0时启动Ⅰ级响应,明确要求“幼儿园、中小学等教育机构停课,停课不停学”.学生和家长对停课这一举措褒贬不一,有为了健康赞成的,有怕耽误学习不赞成的,某调查机构为了了解公众对该举措的态度,随机调查采访了50人,将调查情况整理汇总成如表:
河南多地遭遇年霾,很多学校调整元旦放假时间,提前放假让学生们在家躲霾.郑州市根据《郑州市人民政府办公厅关于将重污染天气黄色预警升级为红色预警的通知》,自12月29日12时将黄色预警升级为红色预警,12月30日0时启动Ⅰ级响应,明确要求“幼儿园、中小学等教育机构停课,停课不停学”.学生和家长对停课这一举措褒贬不一,有为了健康赞成的,有怕耽误学习不赞成的,某调查机构为了了解公众对该举措的态度,随机调查采访了50人,将调查情况整理汇总成如表:| 年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 6 | 9 | 6 | 3 | 4 |
(Ⅱ)若从年龄在[25,35),[65,75]两组采访对象中各随机选取2人进行深度跟踪调查,选中4人中不赞成这项举措的人数为X,求随机变量X的分布列和数学期望.
| A. | $\frac{\sqrt{10}}{5}$ | B. | -$\frac{\sqrt{10}}{5}$ | C. | $\frac{\sqrt{15}}{5}$ | D. | -$\frac{\sqrt{15}}{5}$ |
| 实验操作 | |||||
| 不合格 | 合格 | 良好 | 优秀 | ||
| 体能测试 | 不合格 | 0 | 1 | 1 | 1 |
| 合格 | 0 | 2 | 1 | b | |
| 良好 | 1 | a | 2 | 4 | |
| 优秀 | 1 | 1 | 3 | 6 | |
(Ⅱ)从30人中任意抽取3人,设实验操作考试和体能测试成绩都是良好或优秀的学生人数为X,求随机变量X的分布列及数学期望E(X).
| A. | $-\frac{1}{4}$ | B. | $-\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
 设椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的长轴长为6,离心率$e=\frac{{\sqrt{6}}}{3}$,O为坐标原点.
设椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的长轴长为6,离心率$e=\frac{{\sqrt{6}}}{3}$,O为坐标原点.