题目内容
【题目】如图，给定两个平面单位向量 
和 
，它们的夹角为120°，点C在以O为圆心的圆弧AB上，且 
（其中x，y∈R），则满足x+y≥ 
的概率为（ ） 
A.
B.
C.
D.
【答案】B
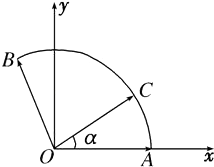
【解析】解：建立如图所示的坐标系，
则A（1，0），B（cos120°，sin120°），
即B（﹣ 
）
设∠AOC=α，则 
=（cosα，sinα）
∵ 
=（x，0）+（﹣ 
， 
）=（cosα，sinα）．
∴ 
∴ 
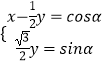
∴x+y= 
sinα+cosα=2sin（α+30°）．
∵0°≤α≤120°．
∴30°≤α+30°≤150°．
当x+y≥ 
时，可得sin（α+30°） 
∴45°≤α+30°≤135°即15°≤α≤105°，
∴满足x+y≥ 的概率P= 
= 
故选B
练习册系列答案
相关题目
