题目内容
设函数f(x)=-x3-2mx2-m2x+1-m(其中m>-2)的图象在x=2处的切线与直线y=-5x+12平行.(1)求m的值;
(2)求函数f(x)在区间[0,1]的最小值;
(3)若a≥0,b≥0,c≥0,且a+b+c=1,试根据上述(1)、(2)的结论证明:
| a |
| 1+a2 |
| b |
| 1+b2 |
| c |
| 1+c2 |
| 9 |
| 10 |
分析:(1)求出函数的导数,f'(x)=-3x2-4mx-m2,函数f(x)图象在x=2处的切线与直线y=-5x+12平行,可得函数f(x)=-x3-2mx2-m2x+1-m的图象在x=2处的切线得斜率为-5,也即f′(2)=-5,代入f'(x)=-3x2-4mx-m2即可求解m的值.
(2)求出函数的f(x)的导数,令f′(x)=0,求出其极值点和单调区间,导数利用导数求解最值.
(3)根据f(x)=-x3+2x2-x+2=(1+x2)(2-x),由(2)的结论,可得
≤
(2-x),再根据已知条件,利用不等式间的等价转化求解.
(2)求出函数的f(x)的导数,令f′(x)=0,求出其极值点和单调区间,导数利用导数求解最值.
(3)根据f(x)=-x3+2x2-x+2=(1+x2)(2-x),由(2)的结论,可得
| 1 |
| 1+x2 |
| 27 |
| 50 |
解答:解:(1)∵f'(x)=-3x2-4mx-m2,所以f'(2)=-12-8m-m2=-5,
解得m=-1或m=-7(舍),即m=-1(3分)
(2)由f'(x)=-3x2+4x-1=0,解得x1=1,x2=
,
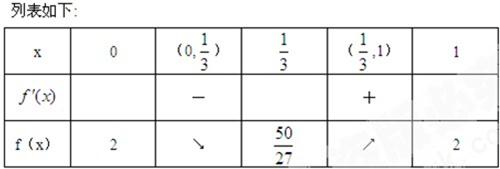
∴函数f(x)在区间[0,1]的最小值为f(
)=
.
(3)∵f(x)=-x3+2x2-x+2=(1+x2)(2-x),
由(2)知,当x∈[0,1]时,(1+x2) (2-x)≥
,
∴
≤
(2-x),
∴
≤
(2x-x2).
当a≥0,b≥0,c≥0,且a+b+c=1时,0≤a≤1,0≤b≤1,0≤c≤1,
所以
+
+
≤
[2(a+b+c)-(a2+b2+c2)]=
[2-(a2+b2+c2)]
又因为(a+b+c)2=a2+b2+c2+2ab+2bc+2ca≤3(a2+b2+c2),
所以a2+b2+c2≥
,
故
+
+
≤
(2-
)=
(当且仅当a=b=c=
时取等号).
解得m=-1或m=-7(舍),即m=-1(3分)
(2)由f'(x)=-3x2+4x-1=0,解得x1=1,x2=
| 1 |
| 3 |

∴函数f(x)在区间[0,1]的最小值为f(
| 1 |
| 3 |
| 50 |
| 27 |
(3)∵f(x)=-x3+2x2-x+2=(1+x2)(2-x),
由(2)知,当x∈[0,1]时,(1+x2) (2-x)≥
| 50 |
| 27 |
∴
| 1 |
| 1+x2 |
| 27 |
| 50 |
∴
| x |
| 1+x2 |
| 27 |
| 50 |
当a≥0,b≥0,c≥0,且a+b+c=1时,0≤a≤1,0≤b≤1,0≤c≤1,
所以
| a |
| 1+a2 |
| b |
| 1+b2 |
| c |
| 1+c2 |
| 27 |
| 50 |
| 27 |
| 50 |
又因为(a+b+c)2=a2+b2+c2+2ab+2bc+2ca≤3(a2+b2+c2),
所以a2+b2+c2≥
| 1 |
| 3 |
故
| a |
| 1+a2 |
| b |
| 1+b2 |
| c |
| 1+c2 |
| 27 |
| 50 |
| 1 |
| 3 |
| 9 |
| 10 |
| 1 |
| 3 |
点评:本题主要考查区间上的最值问题,解题的关键是要对函数进行正确的求导,第三问要求掌握不等式间的等价转化,本题难度比较大,是一道难题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设函数f(x)的定义域为A,若存在非零实数t,使得对于任意x∈C(C⊆A),有x+t∈A,且f(x+t)≤f(x),则称f(x)为C上的t低调函数.如果定义域为[0,+∞)的函数f(x)=-|x-m2|+m2,且 f(x)为[0,+∞)上的10低调函数,那么实数m的取值范围是( )
| A、[-5,5] | ||||||||
B、[-
| ||||||||
C、[-
| ||||||||
D、[-
|