题目内容
已知函数
.
（１）求函数
的单调区间；
（２）设
，求在
上的最大值；
（３）试证明：对任意
，不等式
恒成立．
解：(1)∵
，令
得
，显然
是方程的解
令
，
，则
∴函数
在
上单调递增，∴是方程的唯一解
∵当
时，当
时
∴函数在
上单调递增，在
上单调递减……………………4分
(2)由(1)知函数在上单调递增，在上单调递减
故①当
即
时在上单调递增
∴
＝
②当
时在上单调递减
∴
＝
③当
，即
时
……………………………………………………8分
(3)由（1）知当时，
∴在上恒有
，当且仅当时“＝”成立
∴对任意的恒有
∵
∴
即对
，不等式恒成立．………………….…12分
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
．
的导数
；
上恒成立；
的最大值。
，
的值；
时，求
，
的值．
．
的值；
的单调递增区间．
．
的对称轴方程；
，且
，求
的值．
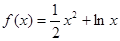
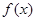在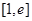
上的最大值和最小值．
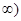，函数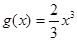
的图象下方。