题目内容

设椭圆的方程是（），离心率为，长轴端点与短轴端点间的距离为.

⑴求椭圆的方程；

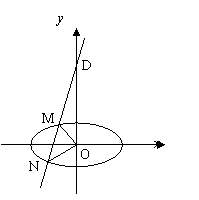⑵是否存在过点的直线与椭圆交于两点，且满足（其中为坐标原点）？若存在，求出直线的方程，若不存在，请说明理由。

解：⑴由已知，，  …………………3分

解得，

所以椭圆的方程为     …………………6分

⑵假设存在满足条件的直线l，其斜率存在，设斜率为k

∴过点满足题意的直线 …………7分

由，消去得，………… 8分

令，解得.  …………………9分

设两点的坐标分别为

则

因为，所以，即

所以

所以 …………………12分

解得.…………………13分

此时满足

综上，过点存在直线与椭圆交于两点，且满足；的方程为  …………………14分

练习册系列答案
相关题目
设中心在原点的椭圆与双曲线2x2-2y2=1有公共的焦点，且它们的离心率互为倒数，则该椭圆的方程是
 
设椭圆的中心是坐标原点，长轴在x轴上，离心率e=
3
2
，已知点P（0，
3
2
）到这个椭圆上的点最远距离是
7
．求这个椭圆的方程，并求椭圆上到点P的距离等于
7
的点的坐标．
（1）若椭圆的方程是：
x2
a2
+
y2
b2
=1（a＞b＞0），它的左、右焦点依次为F1、F2，P是椭圆上异于长轴端点的任意一点．在此条件下我们可以提出这样一个问题：“设△PF1F2的过P角的外角平分线为l，自焦点F2引l的垂线，垂足为Q，试求Q点的轨迹方程？”
对该问题某同学给出了一个正确的求解，但部分解答过程因作业本受潮模糊了，我们在
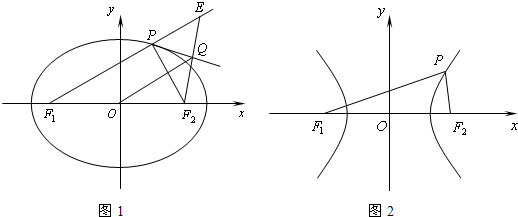
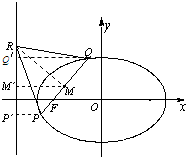精英家教网
这些模糊地方划了线，请你将它补充完整．
解：延长F2Q 交F1P的延长线于E，据题意，
E与F2关于l对称，所以|PE|=|PF2|．
所以|EF1|=|PF1|+|PE|=|PF1|+|PF2|=
 
，
在△EF1F2中，显然OQ是平行于EF1的中位线，
所以|OQ|=
1
2
|EF1|=
 
，
注意到P是椭圆上异于长轴端点的点，所以Q点的轨迹是
 
，
其方程是：
 
．
（2）如图2，双曲线的方程是：
x2
a2
-
y2
b2
=1（a，b＞0），它的左、右焦点依次为F1、F2，P是双曲线上异于实轴端点的任意一点．请你试着提出与（1）类似的问题，并加以证明．
精英家教网设椭圆的方程为
x2
a2
+
y2
b2
=1（a＞b＞0），线段PQ是过左焦点F且不与x轴垂直的焦点弦．若在左准线上存在点R，使△PQR为正三角形，求椭圆的离心率e的取值范围，并用e表示直线PQ的斜率．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网