Question

设椭圆的中心是坐标原点，长轴在x轴上，离心率e=

3

2

，已知点P（0，

3

2

）到这个椭圆上的点最远距离是

7

．求这个椭圆的方程，并求椭圆上到点P的距离等于

7

的点的坐标．

Answer 1

分析：由题设条件取椭圆的参数方程

x=aosθ y=bsinθ

，其中0≤θ＜2π，根据已知条件和椭圆的性质能够推出b=1，a=2．从而求出这个椭圆的方程和椭圆上到点P的距离等于

7

的点的坐标．

解答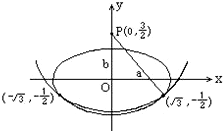：解：根据题设条件，可取椭圆的参数方程是

x=acosθ y=bsinθ

，其中0≤θ＜2π，
由e2=

c2

a2

=1-(

b

a

)2可得

b

a

=

1-e2

=

1- 3 4

=

1

2

，即a=2b．
设椭圆上的点（x，y）到点P的距离为d，则
d2=x2+(y-

3

2

)2
=a2cos2θ+(bsinθ-

3

2

)2
=a2-(a2-b2) sin2θ-3bsinθ+

9

4

=4b2-3b2sin2θ-3bsinθ+

9

4

=-3b2(sinθ+

1

2b

)2+4b2+3．
如果

1

2b

＞1，即b＜

1

2

，则当sinθ=-1时，d²有最大值，由题设得(

7

)2=(b+

3

2

)2，
由此得b=

7

-

3

2

＞

1

2

，与b＜

1

2

矛盾．
因此必有

1

2b

≤1成立，于是当sinθ=-

1

2b

时，d²有最大值，由题设得(

7

)2=4b2+3，
由此可得b=1，a=2．
∴椭圆的方程是

x2

4

+

y2

1

=1，所求椭圆的参数方程是

x=2cosθ y=sinθ

，由sinθ=-

1

2

，cosθ=±

3

2

可得，
椭圆上的点(-

3

，-

1

2

)和(

3

，-

1

2

)到点P的距离都是

7

．

点评：本题考查椭圆的性质及其应用，解题时要注意参数方程的合理运用．