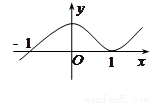题目内容
已知函数 的图象如图所示,
的图象如图所示,直线
 是其两条对称轴.
是其两条对称轴.(1)求函数f(x)的解析式并写出函数的单调增区间;
(2)若f(α)=
 且
且 ,求f(α
,求f(α )的值.
)的值.
【答案】分析:(1)结合函数的图象,求出A,T,然后求出ω,根据极值点求出φ,确定函数f(x)的解析式,利用正弦函数的单调增区间求出函数的单调增区间;
(2)利用f(α)= 且
且 ,求出
,求出 和
和 ,化简f(α
,化简f(α ),然后求出它的值.
),然后求出它的值.
法二:利用f(α)= 且
且 ,求出
,求出 ,然后化简f(α
,然后化简f(α ),求出f(α
),求出f(α )的值.
)的值.
法三:由 得
得 ,求出cos4α,再求出
,求出cos4α,再求出 ,然后化简f(α
,然后化简f(α ),求出f(α
),求出f(α )的值.
)的值.
解答:解:(1)由题意, ,∴T=π,
,∴T=π,
又ω>0,故ω=2,∴f(x)=2sin(2x+φ),(2分)
由 ,解得
,解得 ,
,
又 ,∴
,∴ ,∴
,∴ .(5分)
.(5分)
由 知,
知,
∴函数f(x)的单调增区间为 .(7分)
.(7分)
(2)解法1:依题意得: ,即
,即 ,(8分)
,(8分)
∵ ,∴
,∴ ,
,
∴ ,(10分)
,(10分)

∵
 .(14分)
.(14分)
解法2:依题意得: ,
, 得,①(9分)
得,①(9分)
∵ ,∴
,∴ ,
,
∴ =
= ,(11分)
,(11分)
由 得
得 ②
②
①+②得 ,
,
∴ (14分)
(14分)
解法3:由 得
得 ,(9分)
,(9分)
两边平方得 ,
, ,
,
∵ ∴
∴ ,
,
∴ ,(11分)
,(11分)
∴ ,
,
又 ,∴
,∴ ,
,
∴ .(14分)
.(14分)
点评:本题是基础题,由三角函数的图象确定函数的解析式,利用函数的解析式,求已知函数的三角函数值,求相关角的三角函数值,考查公式的灵活运用能力,化简能力,常考题目.
(2)利用f(α)=
 且
且 ,求出
,求出 和
和 ,化简f(α
,化简f(α ),然后求出它的值.
),然后求出它的值.法二:利用f(α)=
 且
且 ,求出
,求出 ,然后化简f(α
,然后化简f(α ),求出f(α
),求出f(α )的值.
)的值.法三:由
 得
得 ,求出cos4α,再求出
,求出cos4α,再求出 ,然后化简f(α
,然后化简f(α ),求出f(α
),求出f(α )的值.
)的值.解答:解:(1)由题意,
 ,∴T=π,
,∴T=π,又ω>0,故ω=2,∴f(x)=2sin(2x+φ),(2分)
由
 ,解得
,解得 ,
,又
 ,∴
,∴ ,∴
,∴ .(5分)
.(5分)由
 知,
知,
∴函数f(x)的单调增区间为
 .(7分)
.(7分)(2)解法1:依题意得:
 ,即
,即 ,(8分)
,(8分)∵
 ,∴
,∴ ,
,∴
 ,(10分)
,(10分)
∵

 .(14分)
.(14分)解法2:依题意得:
 ,
, 得,①(9分)
得,①(9分)∵
 ,∴
,∴ ,
,∴
 =
= ,(11分)
,(11分)由
 得
得 ②
②①+②得
 ,
,∴
 (14分)
(14分)解法3:由
 得
得 ,(9分)
,(9分)两边平方得
 ,
, ,
,∵
 ∴
∴ ,
,∴
 ,(11分)
,(11分)∴
 ,
,又
 ,∴
,∴ ,
,∴
 .(14分)
.(14分)点评:本题是基础题,由三角函数的图象确定函数的解析式,利用函数的解析式,求已知函数的三角函数值,求相关角的三角函数值,考查公式的灵活运用能力,化简能力,常考题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数的图象如图所示,则其函数解析式可能是( )
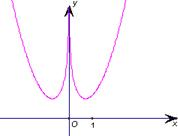

| A、f(x)=x2+ln|x| | B、f(x)=x2-ln|x| | C、f(x)=x+ln|x| | D、f(x)=x-ln|x| |

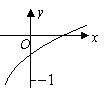 已知函数
已知函数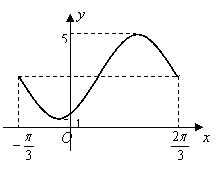
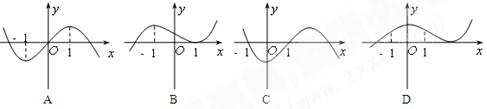
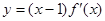 的图象如图所示,其中
的图象如图所示,其中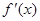 为函数
为函数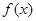 的导函数,则
的导函数,则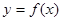 的大致图象是( )
的大致图象是( )