题目内容
已知函数f(x)=x2+ax+b(a,b∈R),不等式|f(x)|≤|2x2+4x-30|对?x∈R恒成立,数列{an}满足: ,
,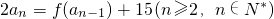 ,数列{bn}满足:
,数列{bn}满足: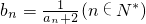 .
.
(Ⅰ)求a,b的值;
(Ⅱ)设数列{bn}的前n和为Sn,前n的积为Tn,求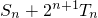 的值.
的值.
解:(Ⅰ)方程2x2+4x-30=0有两实根x=-5或x=3…(1分)
由题意知:当x=-5时,|f(-5)|≤|2•(-5)2+4•(-5)-30|=0,
又∵|f(-5)|≥0,
∴f(-5)=0…(3分)
∴-5是f(x)的一个零点,同理,3也是f(x)的一个零点,…(4分)
∴f(x)=x2+ax+b=(x-3)(x+5)=x2+2x-15,即a=2,b=-15,
显然,|x2+2x-15|≤2|x2+2x-15|对x∈R恒成立.
∴a=2,b=-15…(6分)
(Ⅱ)∵a1= ,2an=f(an-1)+15,
,2an=f(an-1)+15,
∴2an=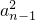 +2an-1=an-1(an-1+2),n=2,3,4,…(7分)
+2an-1=an-1(an-1+2),n=2,3,4,…(7分)
∴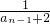 =
=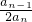 ,n=2,3,4,…,
,n=2,3,4,…,
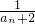 =
= ,n=1,2,3,…
,n=1,2,3,…
∴bn=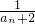 =
= ,…(9分)
,…(9分)
Tn=b1b2…bn=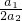 •
•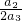 •
•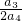 …
…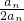
= •
•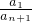
=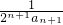 …(10分)
…(10分)
又∵bn=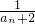 =
= =
=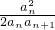 =
=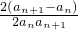 =
= -
- …(12分)
…(12分)
∴Sn=b1+b2+…+bn=( -
- )+(
)+( -
- )+…+(
)+…+( -
- )=
)= -
- =2-
=2- …(13分)
…(13分)
∴2n+1Tn= =2-Sn,
=2-Sn,
∴Sn+2n+1Tn=2为定值. …(14分)
分析:(Ⅰ)由方程2x2+4x-30=0有两实根x=-5或x=3可知,∴-5是与-3是函数f(x)=x2+ax+b的零点,利用韦达定理即可求得a,b的值;
(Ⅱ)由a1= ,2an=f(an-1)+15可求得
,2an=f(an-1)+15可求得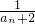 =
=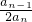 ,结合已知bn=
,结合已知bn=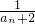 可求得bn=
可求得bn=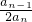 ,从而可求得Tn,对bn=
,从而可求得Tn,对bn=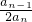 进一步转化可得bn=
进一步转化可得bn= -
- ,继而可求得其前n项和Sn,问题即可解决.
,继而可求得其前n项和Sn,问题即可解决.
点评:本题考查二次函数的零点,数列的求和,考查数列递推公式的应用,突出考查累乘法与裂项法求和的应用,综合性强,难度大,考查创新意识与综合应用能力,属于难题.
由题意知:当x=-5时,|f(-5)|≤|2•(-5)2+4•(-5)-30|=0,
又∵|f(-5)|≥0,
∴f(-5)=0…(3分)
∴-5是f(x)的一个零点,同理,3也是f(x)的一个零点,…(4分)
∴f(x)=x2+ax+b=(x-3)(x+5)=x2+2x-15,即a=2,b=-15,
显然,|x2+2x-15|≤2|x2+2x-15|对x∈R恒成立.
∴a=2,b=-15…(6分)
(Ⅱ)∵a1=
 ,2an=f(an-1)+15,
,2an=f(an-1)+15,∴2an=
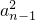 +2an-1=an-1(an-1+2),n=2,3,4,…(7分)
+2an-1=an-1(an-1+2),n=2,3,4,…(7分)∴
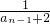 =
=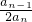 ,n=2,3,4,…,
,n=2,3,4,…,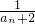 =
= ,n=1,2,3,…
,n=1,2,3,…∴bn=
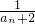 =
= ,…(9分)
,…(9分)Tn=b1b2…bn=
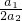 •
•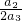 •
•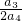 …
…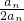
=
 •
•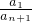
=
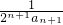 …(10分)
…(10分)又∵bn=
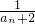 =
= =
=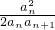 =
=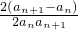 =
= -
- …(12分)
…(12分)∴Sn=b1+b2+…+bn=(
 -
- )+(
)+( -
- )+…+(
)+…+( -
- )=
)= -
- =2-
=2- …(13分)
…(13分)∴2n+1Tn=
 =2-Sn,
=2-Sn,∴Sn+2n+1Tn=2为定值. …(14分)
分析:(Ⅰ)由方程2x2+4x-30=0有两实根x=-5或x=3可知,∴-5是与-3是函数f(x)=x2+ax+b的零点,利用韦达定理即可求得a,b的值;
(Ⅱ)由a1=
 ,2an=f(an-1)+15可求得
,2an=f(an-1)+15可求得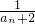 =
=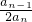 ,结合已知bn=
,结合已知bn=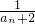 可求得bn=
可求得bn=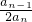 ,从而可求得Tn,对bn=
,从而可求得Tn,对bn=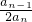 进一步转化可得bn=
进一步转化可得bn= -
- ,继而可求得其前n项和Sn,问题即可解决.
,继而可求得其前n项和Sn,问题即可解决.点评:本题考查二次函数的零点,数列的求和,考查数列递推公式的应用,突出考查累乘法与裂项法求和的应用,综合性强,难度大,考查创新意识与综合应用能力,属于难题.

练习册系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|