题目内容
18.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1、F2,点M(0,$\sqrt{3}$)与点F2的连线交C于点N,且N是线段MF2的中点,F1N⊥MF2,则C的离心率为( )| A. | $\frac{\sqrt{3}+1}{2}$ | B. | $\frac{\sqrt{3}+2}{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{3}$+1 |
分析 运用F1N为MF2的垂直平分线,可得|MF1|=|F1F2|=2c,由对称性可得|MF2|=|MF1|=2c,|NF2|=c,|NF1|=$\sqrt{4{c}^{2}-{c}^{2}}$=$\sqrt{3}$c,再由双曲线的定义和离心率公式,计算即可得到所求值.
解答 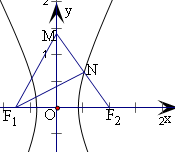 解:N是线段MF2的中点,F1N⊥MF2,
解:N是线段MF2的中点,F1N⊥MF2,
可得F1N为MF2的垂直平分线,
可得|MF1|=|F1F2|=2c,
由对称性可得|MF2|=|MF1|=2c,
|NF2|=c,|NF1|=$\sqrt{4{c}^{2}-{c}^{2}}$=$\sqrt{3}$c,
则2a=|NF1|-|NF2|=$\sqrt{3}$c-c,
可得e=$\frac{c}{a}$=$\frac{2}{\sqrt{3}-1}$=1+$\sqrt{3}$.
故选:D.
点评 本题考查双曲线的离心率的求法,注意运用双曲线的定义和线段的垂直平分线、勾股定理,考查运算能力,属于中档题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
8.命题“?x∈(1,+∞),x3>$\sqrt{x}$”的否定是( )
| A. | ?x0∈(1,+∞),x03$≤\sqrt{{x}_{0}}$ | B. | ?x∈(1,+∞),x3$≤\sqrt{x}$ | ||
| C. | ?x0∈(-∞,1],x03≤$\sqrt{{x}_{0}}$ | D. | ?x∈(-∞,1],x3≤$\sqrt{x}$ |
6.已知sinα+sinβ+sinγ=0和cosα+cosβ+cosγ=0,则cos(α-β)的值是( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
8.已知$\frac{a+i}{i}$=b+2i(a,b∈R),其中为虚数单位,则a-b=( )
| A. | -3 | B. | -2 | C. | -1 | D. | 1 |