题目内容
15.已知函数f(x)=2x+$\frac{1}{x}$+λlnx(x>0).(1)若x=1是函数f(x)的一个极值点,求λ的值;
(2)求函数f(x)极值的个数;
(3)若对于任意两个不相等的正数x1,x2均有|f′(x1)-f′(x2)|<|x1-x2|恒成立,求实数λ的取值范围.
分析 (1)求出函数f(x)的导数,由题意可得f′(1)=0,可得λ的值;
(2)求出f(x)的导数,对λ讨论,结合函数的定义域,即可得到极值个数;
(3)求出导数,代入化简整理可得|$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$-λ|<x1x2,运用不等式的性质,即可得到所求范围.
解答 解:(1)函数f(x)=2x+$\frac{1}{x}$+λlnx(x>0)的导数为f′(x)=2-$\frac{1}{{x}^{2}}$+$\frac{λ}{x}$,
若x=1是函数f(x)的一个极值点,则f′(1)=0,
即为2-1+λ=0,解得λ=-1;
(2)函数f(x)=2x+$\frac{1}{x}$+λlnx(x>0)的导数为f′(x)=2-$\frac{1}{{x}^{2}}$+$\frac{λ}{x}$
=$\frac{2{x}^{2}+λx-1}{{x}^{2}}$,
令g(x)=2x2+λx-1,由g(x)=0,可得x=$\frac{-λ±\sqrt{{λ}^{2}+8}}{4}$,
当λ=0时,x=$±\frac{\sqrt{2}}{2}$,由x>0,可得只有一个极值;
当λ>0时,g(x)=0的解只有一个正解,即极值只有一个;
当λ<0时,g(x)=0的解只有一个正解,即极值只有一个.
综上可得,函数f(x)极值的个数为1;
(3)若对于任意两个不相等的正数x1,x2均有|f′(x1)-f′(x2)|<|x1-x2|恒成立,
即为|2-$\frac{1}{{{x}_{1}}^{2}}$+$\frac{λ}{{x}_{1}}$-2+$\frac{1}{{{x}_{2}}^{2}}$-$\frac{λ}{{x}_{2}}$|<|x1-x2|恒成立,
化简可得|$\frac{{x}_{1}+{x}_{2}}{{{x}_{1}}^{2}{{x}_{2}}^{2}}$-$\frac{λ}{{x}_{1}{x}_{2}}$|<1,即有|$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$-λ|<x1x2,
即为$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$-x1x2<λ<$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$+x1x2恒成立,
由$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$+x1x2>3$\root{3}{\frac{1}{{x}_{1}}•\frac{1}{{x}_{2}}•{x}_{1}{x}_{2}}$=3,$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$-x1x2无最值.
即有实数λ的取值范围是(-∞,3].
点评 本题考查导数的运用:求单调区间和极值、最值,同时考查分类讨论的思想方法和不等式恒成立问题的解决方法,属于中档题.

 智慧小复习系列答案
智慧小复习系列答案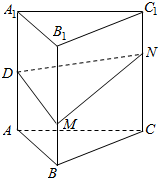 如图,正三棱柱ABC-A1B1C1(底面是正三角形,侧棱垂直底面)的各条棱长均相等,D为AA1的中点.M、N分别是BB1、CC1上的动点(含端点),且满足BM=C1N.当M,N运动时,下列结论中不正确的是( )
如图,正三棱柱ABC-A1B1C1(底面是正三角形,侧棱垂直底面)的各条棱长均相等,D为AA1的中点.M、N分别是BB1、CC1上的动点(含端点),且满足BM=C1N.当M,N运动时,下列结论中不正确的是( )| A. | 平面DMN⊥平面BCC1B1 | |
| B. | 三棱锥A1-DMN的体积为定值 | |
| C. | △DMN可能为直角三角形 | |
| D. | 平面DMN与平面ABC所成的锐二面角范围为(0,$\frac{π}{4}$] |
| A. | $\frac{3π}{5}$ | B. | $\frac{6π}{5}$ | C. | $\frac{9π}{5}$ | D. | $\frac{12π}{5}$ |
 如图所示,ABFC-A1B1F1C1为正四棱柱,D为BC上一点,且A1B∥平面AC1D,D1是B1C1的中点,BC1⊥AB1,BC1⊥A1C.求证:
如图所示,ABFC-A1B1F1C1为正四棱柱,D为BC上一点,且A1B∥平面AC1D,D1是B1C1的中点,BC1⊥AB1,BC1⊥A1C.求证: