题目内容
5.若cosα=$\frac{1}{3}$,则sin$({\frac{π}{2}+2α})$-$\frac{7}{9}$.分析 由诱导公式和二倍角的正弦函数公式化简所求后根据已知即可求值.
解答 解:∵cosα=$\frac{1}{3}$,
∴sin$({\frac{π}{2}+2α})$=cos2α=2cos2α-1=2×$\frac{1}{9}-1$=-$\frac{7}{9}$.
故答案为:-$\frac{7}{9}$.
点评 本题主要考查了诱导公式和二倍角的正弦函数公式的应用,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.已知f(x)=sin(2015x+$\frac{3π}{8}$)+sin(2015x-$\frac{π}{8}$)的最大值为A,若存在实数x1,x2,使得对任意实数x总有f(x1)≤f(x)≤f(x2)成立,则A|x1-x2|的最小值为( )
| A. | $\frac{\sqrt{2}π}{2015}$ | B. | $\frac{2\sqrt{2}π}{2015}$ | C. | $\frac{2π}{2015}$ | D. | $\frac{4π}{2015}$ |
17.已知某几何体的三视图如图所示,则该几何体的体积为( )
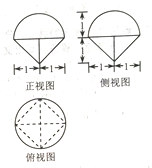

| A. | $\frac{2}{3}({π+1})$ | B. | $\frac{4}{3}$(π+1) | C. | $\frac{4}{3}$(π+$\frac{1}{2}$) | D. | $\frac{2}{3}$(π+$\frac{1}{2}$) |
14.如果函数y=|cos(ωx+$\frac{π}{4}$)|的图象关于直线x=π对称,则正实数ω的最小值是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
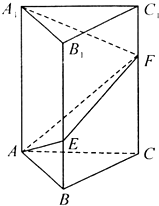 如图,在直三棱柱ABC-A1B1C1中,已知∠BAC=90°,AB=AC=1,AA1=3,点E,F分别在棱BB1,CC1上,且C1F=$\frac{1}{3}$C1C,BE=$\frac{1}{3}$BB1.
如图,在直三棱柱ABC-A1B1C1中,已知∠BAC=90°,AB=AC=1,AA1=3,点E,F分别在棱BB1,CC1上,且C1F=$\frac{1}{3}$C1C,BE=$\frac{1}{3}$BB1.