题目内容
设函数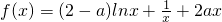 .
.
(1)当a=0时,求f(x)的极值;
(2)当a≠0时,求f(x)的单调区间;
(3)当a=2时,对任意的正整数n,在区间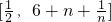 上总有m+4个数使得f(a1)+f(a2)+f(a3)+…+f(am)<f(am+1)+f(am+2)+f(am+3)+f(am+4)成立,试求正整数m的最大值.
上总有m+4个数使得f(a1)+f(a2)+f(a3)+…+f(am)<f(am+1)+f(am+2)+f(am+3)+f(am+4)成立,试求正整数m的最大值.
解:(1)函数f(x)的定义域为(0,+∞).…(1分)
当a=0时,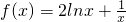 ,∴
,∴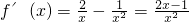 .…(2分)
.…(2分)
由f'(x)=0得 .
.
f(x),f'(x)随x变化如下表:
故,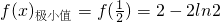 ,没有极大值.…(4分)
,没有极大值.…(4分)
(2)由题意,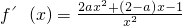
令f'(x)=0得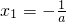 ,
, .…(6分)
.…(6分)
若a>0,由f'(x)≤0得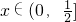 ;由f'(x)≥0得
;由f'(x)≥0得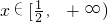 .…(7分)
.…(7分)
若a<0,①当a<-2时,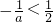 ,
,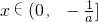 或
或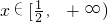 ,f'(x)≤0;
,f'(x)≤0;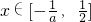 ,f'(x)≥0,
,f'(x)≥0,
②当a=-2时,f'(x)≤0
③当-2<a<0时,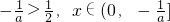 或
或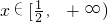 ,f'(x)≤0;
,f'(x)≤0;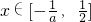 ,f'(x)≥0.
,f'(x)≥0.
综上,当a>0时,函数的单调递减区间为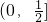 ,单调递增区间为
,单调递增区间为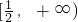 ;
;
当a<-2时,函数的单调递减区间为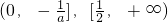 ,单调递增区间为
,单调递增区间为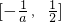 ;
;
当-2<a<0时,函数的单调递减区间为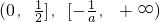 ,单调递增区间为
,单调递增区间为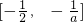 …(10分)
…(10分)
(3)当a=2时,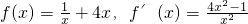 .
.
∵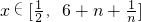 ,∴f'(x)≥0
,∴f'(x)≥0
∴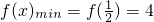 ,
,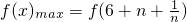 .…(12分)
.…(12分)
由题意,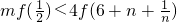 恒成立.
恒成立.
令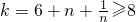 ,且f(k)在
,且f(k)在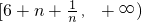 上单调递增,
上单调递增,
∴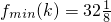 ,因此
,因此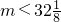 ,而m是正整数,故m≤32,
,而m是正整数,故m≤32,
所以,m=32时,存在 ,am+1=am+2=am+2=am+4=8时,对所有n满足题意,∴mmax=32.
,am+1=am+2=am+2=am+4=8时,对所有n满足题意,∴mmax=32.
分析:(1)求导函数,确定函数的单调性,进而可求f(x)的极值;
(2)求导函数,利用导数的正负,分类讨论,即可确定函数的单调区间;
(3)当a=2时,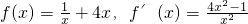 ,求出函数的最值,问题转化为
,求出函数的最值,问题转化为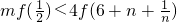 恒成立.
恒成立.
令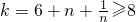 ,且f(k)在
,且f(k)在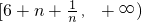 上单调递增,由此可求正整数m的最大值.
上单调递增,由此可求正整数m的最大值.
点评:本题考查导数知识的运用,考查函数的极值与单调性,考查分类讨论的数学思想,考查恒成立问题,正确求导是关键.
当a=0时,
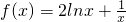 ,∴
,∴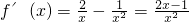 .…(2分)
.…(2分)由f'(x)=0得
 .
.f(x),f'(x)随x变化如下表:
| x |  |  | 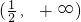 |
| f(x) | - | 0 | + |
| f'(x) | ↘ | 极小值 | ↙ |
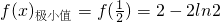 ,没有极大值.…(4分)
,没有极大值.…(4分)(2)由题意,
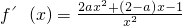
令f'(x)=0得
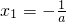 ,
, .…(6分)
.…(6分)若a>0,由f'(x)≤0得
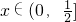 ;由f'(x)≥0得
;由f'(x)≥0得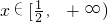 .…(7分)
.…(7分)若a<0,①当a<-2时,
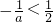 ,
,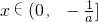 或
或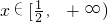 ,f'(x)≤0;
,f'(x)≤0;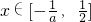 ,f'(x)≥0,
,f'(x)≥0,②当a=-2时,f'(x)≤0
③当-2<a<0时,
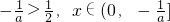 或
或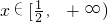 ,f'(x)≤0;
,f'(x)≤0;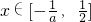 ,f'(x)≥0.
,f'(x)≥0.综上,当a>0时,函数的单调递减区间为
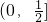 ,单调递增区间为
,单调递增区间为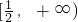 ;
;当a<-2时,函数的单调递减区间为
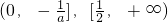 ,单调递增区间为
,单调递增区间为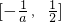 ;
;当-2<a<0时,函数的单调递减区间为
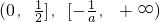 ,单调递增区间为
,单调递增区间为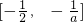 …(10分)
…(10分)(3)当a=2时,
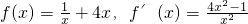 .
.∵
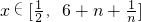 ,∴f'(x)≥0
,∴f'(x)≥0∴
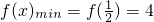 ,
,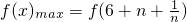 .…(12分)
.…(12分)由题意,
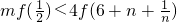 恒成立.
恒成立.令
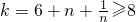 ,且f(k)在
,且f(k)在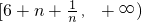 上单调递增,
上单调递增,∴
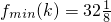 ,因此
,因此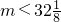 ,而m是正整数,故m≤32,
,而m是正整数,故m≤32,所以,m=32时,存在
 ,am+1=am+2=am+2=am+4=8时,对所有n满足题意,∴mmax=32.
,am+1=am+2=am+2=am+4=8时,对所有n满足题意,∴mmax=32.分析:(1)求导函数,确定函数的单调性,进而可求f(x)的极值;
(2)求导函数,利用导数的正负,分类讨论,即可确定函数的单调区间;
(3)当a=2时,
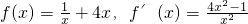 ,求出函数的最值,问题转化为
,求出函数的最值,问题转化为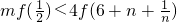 恒成立.
恒成立.令
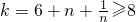 ,且f(k)在
,且f(k)在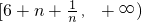 上单调递增,由此可求正整数m的最大值.
上单调递增,由此可求正整数m的最大值.点评:本题考查导数知识的运用,考查函数的极值与单调性,考查分类讨论的数学思想,考查恒成立问题,正确求导是关键.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
 。
。 的极值;
的极值; 2时,讨论函数
2时,讨论函数 成立,求
成立,求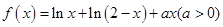 。
。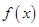 的单调区间。
的单调区间。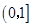 上的最大值为
上的最大值为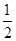 ,求a的值。
,求a的值。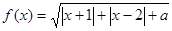 。
。 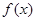 的定义域。
的定义域。 。
。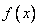 的单调区间。
的单调区间。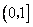 上的最大值为
上的最大值为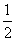 ,求a的值。
,求a的值。