题目内容
【题目】已知数列{an}是等比数列,且满足a2+a5=36,a3a4=128. (Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{an}是递增数列,且bn=an+log2an(n∈N*),求数列{bn}的前n项和Sn .
【答案】解:(Ⅰ)∵数列{an}是等比数列,且满足a2+a5=36,a3a4=128. ∴a2a5=a3a4=128,
联立 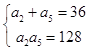 ,
,
解得 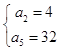 或
或 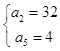 ,
,
解得 ![]() 或
或 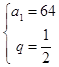 .
.
∴an=2n , 或 ![]() .
.
(Ⅱ)∵数列{an}是递增数列,∴ ![]() ,
,
∴bn=an+log2an
=2n+n,
∴数列{bn}的前n项和Sn=(2+22+…+2n)+(1+2+…+n)
= ![]() +
+ ![]()
=2n+1﹣2+ ![]() .
.
【解析】(Ⅰ)数列{an}是等比数列,且满足a2+a5=36,a3a4=128.可得a2a5=a3a4=128,再利用等比数列的通项公式即可得出;(Ⅱ)利用等差数列与等比数列前n项和公式即可得出.
【考点精析】根据题目的已知条件,利用等比数列的通项公式(及其变式)和数列的前n项和的相关知识可以得到问题的答案,需要掌握通项公式:![]() ;数列{an}的前n项和sn与通项an的关系
;数列{an}的前n项和sn与通项an的关系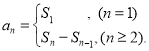 .
.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案
相关题目