题目内容
【题目】设常数![]() .
.
(1)若![]() 在
在![]() 处取得极小值为
处取得极小值为![]() ,求
,求![]() 和
和![]() 的值;
的值;
(2)对于任意给定的正实数![]() 、
、![]() ,证明:存在实数
,证明:存在实数![]() ,当
,当![]() 时,
时, ![]() .
.
【答案】(1)![]() .(2)见解析
.(2)见解析
【解析】试题分析:(1)本问考查极值点导数为,根据极值点导数为0,对函数求导, 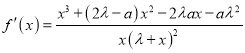 ,
, ![]() ,
, ![]() ,再根据
,再根据![]() ,可以求出
,可以求出![]() 的值;(2)本问考查存在性问题的证明,主要是将问题进行转化,
的值;(2)本问考查存在性问题的证明,主要是将问题进行转化, ![]() ,记
,记![]() ,故只需证明:存在实数
,故只需证明:存在实数![]() ,当
,当![]() 时,
时, ![]() ,而
,而 ![]() ,设
,设![]() ,通过证明得到恒有
,通过证明得到恒有![]() .即当
.即当![]() 时, 恒有
时, 恒有![]() 成立.
成立.
试题解析:(1)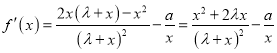
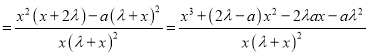 ,
,
∵![]() ,∴
,∴![]() .
.
将![]() 代入得
代入得
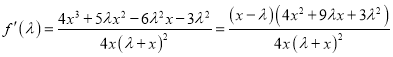
当![]() 时,
时, ![]() ,
, ![]() 递减;
递减;
![]() 时,
时, ![]() ,
, ![]() 递增;
递增;
故当![]() 时,
时, ![]() 取极小值
取极小值![]() ,
,
令![]() ,解得
,解得![]() .
.
(Ⅱ)因为![]() ,
,
记![]() ,故只需证明:存在实数
,故只需证明:存在实数![]() ,当
,当![]() 时,
时, ![]() ,
,
[方法1] ![]() ,
,
设![]() ,则
,则![]() .
.
易知当![]() 时,
时, ![]() ,故
,故![]() .
.
又由![]() 解得:
解得: ![]() ,即
,即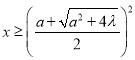
取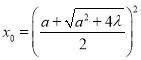 ,则当
,则当![]() 时, 恒有
时, 恒有![]() .
.
即当![]() 时, 恒有
时, 恒有![]() 成立.
成立.
[方法2] 由![]() ,得:
,得: ![]() ,
,
故![]() 是区间
是区间![]() 上的增函数.令
上的增函数.令![]() ,
,
则![]() ,因为
,因为![]() ,
,
故有![]() ,
,
令![]() ,解得:
,解得: 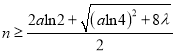 ,
,
设![]() 是满足上述条件的最小正整数,取
是满足上述条件的最小正整数,取![]() ,则当
,则当![]() 时, 恒有
时, 恒有![]() ,
,
即![]() 成立.
成立.

练习册系列答案
相关题目