题目内容
11.已知函数f(x)=sin|ωx|,若y=f(x)与y=m(m为常数)图象的公共点中,相邻两个公共点的距离的最大值为2π,则ω的值为( )| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
分析 通过函数f(x)=sinωx关于y轴对称画出函数f(x)=sin|ωx|图象,相邻两个交点的距离的最大值为f(x)=sinωx的周期的$\frac{3}{2}$.利用周期公式建立关系求解即可.
解答 解:由函数f(x)=sinωx关于y轴对称可得函数f(x)=sin|ωx|图象 ,
,
相邻两个公共点的距离的最大值为2π,即相邻两个交点的距离的最大值为f(x)=sinωx的周期的$\frac{3}{2}$.
故得:$2π=\frac{3}{2}T=\frac{2π}{ω}×\frac{3}{2}$,
解得:ω=$\frac{3}{2}$.
故选C.
点评 本题主要考查三角函数的图象和性质的运用,图象的对称翻折问题,利用了数形结合法,属于中档题.

练习册系列答案
相关题目
19.表面积为$\frac{{4\sqrt{3}}}{3}$的正四面体的各个顶点都在同一个球面上,则此球的体积为( )
| A. | $\frac{{\sqrt{2}}}{3}π$ | B. | $\frac{1}{3}π$ | C. | $\frac{2}{3}π$ | D. | $\frac{{2\sqrt{2}}}{3}π$ |
6.函数f(x)=$\frac{a{x}^{3}}{3}$+$\frac{a{x}^{2}}{2}$-2ax+2a+1的图象经过四个象限,则实数a的取值范围是( )
| A. | (-$\frac{6}{5}$,$\frac{3}{16}$) | B. | (-$\frac{8}{5}$,-$\frac{3}{16}$) | C. | (-$\frac{8}{5}$,-$\frac{1}{16}$) | D. | (-$\frac{6}{5}$,-$\frac{3}{16}$) |
16.已知f(x)是定义在区间(0,+∞)上的函数,其导函数为f'(x),且不等式xf'(x)<2f(x)恒成立,则( )
| A. | 4f(1)<f(2) | B. | 4f(1)>f(2) | C. | f(1)<4f(2) | D. | f(1)<2f'(2) |
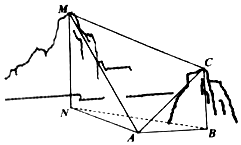 如图,为测量山高l,选择A和另一座山的山顶|PA|为测量观测点.从MB=MC点测得△ABC点的仰角60°,C点的仰角45°以及∠MAC=75°;从C点测得∠MCA=60°.已知山高BC=100m,则山高MN=150m.
如图,为测量山高l,选择A和另一座山的山顶|PA|为测量观测点.从MB=MC点测得△ABC点的仰角60°,C点的仰角45°以及∠MAC=75°;从C点测得∠MCA=60°.已知山高BC=100m,则山高MN=150m.