题目内容
17．
如图，它满足第n行首尾两数均为n，则第7行第2个数是22．第n行（n≥2）第2个数是$\frac{{n}^{2}-n+2}{2}$．
分析 设第7行第2个数是x，由斜列：2，4，7，11，16，…，可知4-2=2，7-4=3，11-7=4，16-11=5，x-16=6，解得x．由a2=2，a3=4，a4=7，a5=11，…，可得：a3-a2=2，a4-a3=3，a5-a4=4，…，利用“累加求和”方法即可得出．
解答 解：①设第7行第2个数是x，由斜列：2，4，7，11，16，…，可知4-2=2，7-4=3，11-7=4，16-11=5，x-16=6，解得x=22．
②由a2=2，a3=4，a4=7，a5=11，…，
可得：a3-a2=4-2=2，a4-a3=7-4=3，a5-a4=11-7=4，…，
∴an=a2+（a3-a2）+（a4-a3）+…+（an-an-1）
=2+2+3+…+（n-1）
=1+$\frac{n（n-1）}{2}$
=$\frac{{n}^{2}-n+2}{2}$．
故答案分别为：22；$\frac{{n}^{2}-n+2}{2}$．
点评 本题考查了“累加求和”方法、等差数列的前n项和公式，考查了推理能力与计算能力，属于中档题．
练习册系列答案
导学教程高中新课标系列答案
小学课时特训系列答案
相关题目
5．当x→0时，下列四个无穷小阶数最高的是（ ）
| A． | e${\;}^{{x}^{4}-{x}^{3}}$-1 | B． | cosx2-1 | C． | $\sqrt{1+{x}^{2}}$-1 | D． | tanx-sinx |
2．如图所示，在棱长为1的正方体ABCD-A1B1C1D1中，P是A1B上一动点，则AP+D1P的最小值为（ ）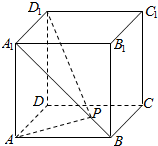
| A． | 2 | B． | $\frac{{\sqrt{6}+\sqrt{2}}}{2}$ | C． | $2+\sqrt{2}$ | D． | $\sqrt{2+\sqrt{2}}$ |
9．
如图是函数$f（x）=Asin（2x+ϕ），（A＞0，|ϕ|≤\frac{π}{2}）$图象的一部分，对不同的x1，x2∈[a，b]，若f（x1）=f（x2），有$f（{x_1}+{x_2}）=\sqrt{2}$，则（ ）
如图是函数$f（x）=Asin（2x+ϕ），（A＞0，|ϕ|≤\frac{π}{2}）$图象的一部分，对不同的x1，x2∈[a，b]，若f（x1）=f（x2），有$f（{x_1}+{x_2}）=\sqrt{2}$，则（ ）| A． | f（x）在$（-\frac{3π}{8}，\frac{π}{8}）$上是增函数 | B． | f（x）在$（-\frac{3π}{8}，\frac{π}{8}）$上是减函数 | ||
| C． | f（x）在$（-\frac{5π}{12}，\frac{π}{12}）$上是增函数 | D． | f（x）在$（-\frac{5π}{12}，\frac{π}{12}）$上是减函数 |