题目内容
在三角形ABC中,下列等式总能成立的是
- A.a cosC=c cosA
- B.bsinC=csinA
- C.absinc=bcsinB
- D.asinC=csinA
D
试题分析:A:由正弦定理可得,acosC-ccosA=2RsinAcosC-2RsinCcosA=2Rsin(A-C)=0不一定成立,
即acosC="ccosA" 不一定成立,A错误
B:由正弦定理可得,bsinC-csinA=2RsinBsinC-2RsinCsinA=2RsinC(sinB-sinC)=0不一定成立,即bsinC=csinA不一定成立,B错误
C:由正弦定理可得absinC-bcsinB=2bR(sinAsinC-sinCsinB)=2bRsinC(sinA-sinB)=0不一定成立,即absinC=bcsinB不一定成立,C错误
D:由正弦定理可得,asinC-csinA=2RsinAsinC-2RsinCsinA=0,即asinC=csinA一定成立,D正确
故选D
考点:本题主要考查正弦定理、余弦定理的应用。
点评:利用正弦定理、余弦定理对选项进行分析。
试题分析:A:由正弦定理可得,acosC-ccosA=2RsinAcosC-2RsinCcosA=2Rsin(A-C)=0不一定成立,
即acosC="ccosA" 不一定成立,A错误
B:由正弦定理可得,bsinC-csinA=2RsinBsinC-2RsinCsinA=2RsinC(sinB-sinC)=0不一定成立,即bsinC=csinA不一定成立,B错误
C:由正弦定理可得absinC-bcsinB=2bR(sinAsinC-sinCsinB)=2bRsinC(sinA-sinB)=0不一定成立,即absinC=bcsinB不一定成立,C错误
D:由正弦定理可得,asinC-csinA=2RsinAsinC-2RsinCsinA=0,即asinC=csinA一定成立,D正确
故选D
考点:本题主要考查正弦定理、余弦定理的应用。
点评:利用正弦定理、余弦定理对选项进行分析。

练习册系列答案
相关题目
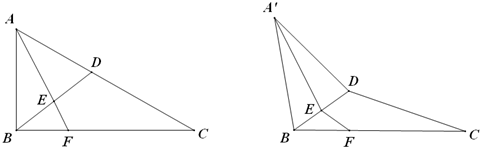

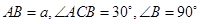 , D为AC的中点,E为BD的中点,AE的延长线交BC于F,将△ABD沿BD折起,二面角
, D为AC的中点,E为BD的中点,AE的延长线交BC于F,将△ABD沿BD折起,二面角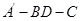 的大小记为
的大小记为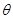 .
.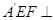 平面BCD;
平面BCD;
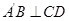 时,求
时,求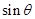 的值;
的值;
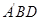 的距离.
的距离.