Question

如果关于x的方程a(b－c)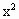＋b(c－a)x＋c(a－b)＝0有两个相等的实根(abc≠0)，求证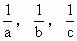：成等差数列．

Answer 1

答案：
解析：

当x＝1时，a(b－c)＋b(c－a)＋c(a－b)＝0，又方程有两个相等的实根，∴＝1，于是＝1，∴c(a－b)＝a(b－c)，即2ac＝ab＋bc，两边同除以abc，得．∴，，成等差数列．