题目内容
所有真约数(除本身之外的正约数)的和等于它本身的正整数叫做完全数.
如: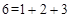 ;
;
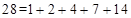 ;
;
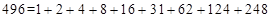 .
.
已经证明:若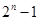 是质数,则
是质数,则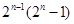 是完全数,
是完全数,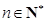 .请写出一个四位完全数 ;又
.请写出一个四位完全数 ;又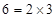 ,所以
,所以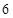 的所有正约数之和可表示为
的所有正约数之和可表示为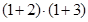 ;
;
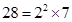 ,所以
,所以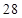 的所有正约数之和可表示为
的所有正约数之和可表示为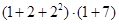 ;
;
按此规律,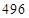 的所有正约数之和可表示为 .
的所有正约数之和可表示为 .
如:
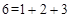 ;
;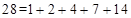 ;
;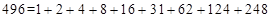 .
.已经证明:若
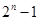 是质数,则
是质数,则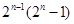 是完全数,
是完全数,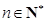 .请写出一个四位完全数 ;又
.请写出一个四位完全数 ;又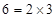 ,所以
,所以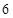 的所有正约数之和可表示为
的所有正约数之和可表示为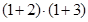 ;
;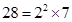 ,所以
,所以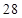 的所有正约数之和可表示为
的所有正约数之和可表示为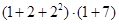 ;
;按此规律,
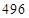 的所有正约数之和可表示为 .
的所有正约数之和可表示为 . ;
;
试题分析:(1)由若
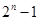 是质数,则
是质数,则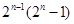 是完全数可知,
是完全数可知, 是质数,所以
是质数,所以 是完全数。(2)因为
是完全数。(2)因为 ,所以
,所以 的所有正约数之和可表示为
的所有正约数之和可表示为

练习册系列答案
相关题目
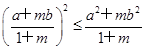 .
.
 (x>0),观察:f1(x)=f(x)=
(x>0),观察:f1(x)=f(x)= ,f3(x)=f(f2(x))=
,f3(x)=f(f2(x))= ,故fn(x)= .
,故fn(x)= . 表示不超过
表示不超过 的最大整数.
的最大整数.
 .
.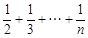 (n∈N*),经计算得f(4)>2,f(8)>
(n∈N*),经计算得f(4)>2,f(8)> ,f(16)>3,f(32)>
,f(16)>3,f(32)> ,……,观察上述结果,则可归纳出一般结论为 。
,……,观察上述结果,则可归纳出一般结论为 。 中,
中, ,斜边
,斜边 上的高为h1,则
上的高为h1,则 ;类比此性质,如图,在四面体
;类比此性质,如图,在四面体 中,若
中,若 ,
, ,
, 两两垂直,底面
两两垂直,底面 上的高为
上的高为 ,则得到的正确结论为_________________________.
,则得到的正确结论为_________________________.
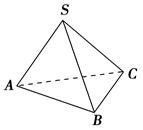
 ,类似地正四面体的中心与四个顶点连线所成的四个张角也相等,其余弦值为( )。
,类似地正四面体的中心与四个顶点连线所成的四个张角也相等,其余弦值为( )。


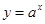 是增函数;
是增函数;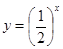 是指数函数;
是指数函数;