题目内容
在△ABC中，C=120°，tanA+tanB=
，则tanAtanB的值为
．
2
| ||
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
分析：利用和角的正切公式，结合已知条件，即可求得tanAtanB的值．
解答：解：∴tan（A+B）=
∴1-tanAtanB=
∵△ABC中，C=120°，tanA+tanB=
∴1-tanAtanB=
∴tanAtanB=
故答案为：
| tanA+tanB |
| 1-tanAtanB |
∴1-tanAtanB=
| tanA+tanB |
| tan(A+B) |
∵△ABC中，C=120°，tanA+tanB=
2
| ||
| 3 |
∴1-tanAtanB=
| ||||
|
∴tanAtanB=
| 1 |
| 3 |
故答案为：
| 1 |
| 3 |
点评：本题考查和角的正切公式，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
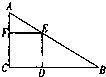如图所示，已知在△ABC中，∠C=90°，正方形DEFC内接于△ABC，DE∥AC，EF∥BC，AC=1，BC=2，则AF：FC=
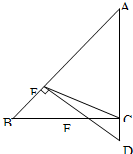（2004•上海模拟）如图，在△ABC中，∠C=90°，sinB=