题目内容
设函数![]() 为实数).
为实数).
(Ⅰ)若![]() 为偶函数,求实数a的值;
为偶函数,求实数a的值;
(Ⅱ)设![]() ,求函数
,求函数![]() 的最小值.
的最小值.
解:(Ⅰ)![]() 函数
函数![]() 是偶函数,
是偶函数,
![]()
![]() ,即
,即![]() ,解得
,解得![]() ;………………………………… 3分
;………………………………… 3分
![]()
![]() (Ⅱ)
(Ⅱ)![]() =
= 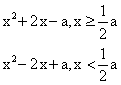 ,………………………………………………… 5分
,………………………………………………… 5分
当![]() 时,
时,![]() ,
,
由![]() ,得
,得![]() ,
,
故![]() 在
在![]() 时单调递增,
时单调递增,![]() 的最小值为
的最小值为![]() ;……………………… 8分
;……………………… 8分
![]() ‚当
‚当![]() ,
,![]() ,
,
故当![]() 时,
时,![]() 单调递增,当
单调递增,当![]() 时,
时,![]() 单调递减,
单调递减,
则![]() 的最小值为
的最小值为![]() ;……………………………………………………… 11分
;……………………………………………………… 11分
由于![]() ,故
,故![]() 的最小值为
的最小值为![]() . ………………………… 12分
. ………………………… 12分

练习册系列答案
相关题目
 为实数。
为实数。 在
在 处取得极值,求
处取得极值,求 的值;
的值;
 对任意
对任意 都成立,求实数
都成立,求实数 的取值范围。
的取值范围。