题目内容
等差数列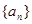 的前
的前 项和记为
项和记为 ,已知
,已知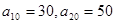 .
.
(1)求数列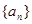 的通项
的通项 ;
;
(2)若 ,求
,求 ;
;
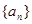 的前
的前 项和记为
项和记为 ,已知
,已知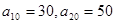 .
.(1)求数列
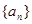 的通项
的通项 ;
;(2)若
 ,求
,求 ;
;(1) ;(2)n=11.
;(2)n=11.
 ;(2)n=11.
;(2)n=11.试题分析:(1)由等差数列的通项公式求出首项和公差.利用通项公式写出通项.(2)通过(1)求出的首项和公差,利用等差数列的求和公式求出n.本题主要是对等差数列的通项和前n项和公式的应用.属于基础简单题型.
试题解析:(1)由
 ,得方程组
,得方程组 ,
,解得


(2)由

得方程

解得
 或
或 (舍去)
(舍去)
练习册系列答案
相关题目
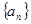 具有性质:①
具有性质:①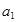 为正数;②对于任意的正整数
为正数;②对于任意的正整数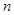 ,当
,当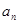 为偶数时,
为偶数时,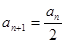 ;当
;当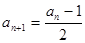
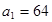 ,求数列
,求数列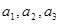 成等差数列,求
成等差数列,求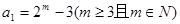 ,数列
,数列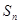 ,求证:
,求证: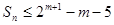
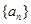 的前
的前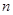 项和为
项和为 ,且
,且 .
. 求证:
求证: .
.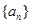 的前n项和为
的前n项和为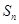 ,已知
,已知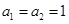 ,
,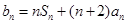 ,数列
,数列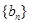 是公差为d的等差数列,
是公差为d的等差数列,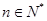 .
.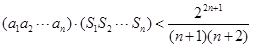 .
.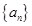 ,等比数列
,等比数列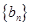 中,
中,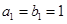 ,
,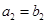 ,
,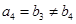 .
.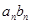 ;
;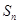 为数列
为数列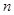 项和,
项和,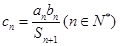 ,
,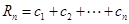 ,求
,求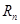 .
. 的前n项和为
的前n项和为 ,且
,且 ,
, .
.  ;
; ,求数列
,求数列 的前n项和
的前n项和 .
.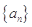 的前n项和为
的前n项和为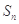 ,已知
,已知 ,
,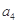 是
是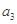 和
和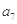 的等比中项.
的等比中项. 为等差数列,且
为等差数列,且 ,则数列
,则数列 ( )
( )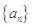 中,
中,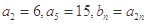 ,则数列
,则数列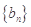 的前5项和
的前5项和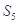 =______.
=______.