题目内容
设a∈[-2,0],已知函数f(x)=
(Ⅰ) 证明f(x)在区间(-1,1)内单调递减,在区间(1,+∞)内单调递增;
(Ⅱ) 设曲线y=f(x)在点Pi(xi,f(xi))(i=1,2,3)处的切线相互平行,且x1x2x3≠0,证明x1+x2+x3>
.
|
(Ⅰ) 证明f(x)在区间(-1,1)内单调递减,在区间(1,+∞)内单调递增;
(Ⅱ) 设曲线y=f(x)在点Pi(xi,f(xi))(i=1,2,3)处的切线相互平行,且x1x2x3≠0,证明x1+x2+x3>
| 1 |
| 3 |
(I)令f1(x)=x3-(a+5)x(x≤0),f2(x)=x3-
x2+ax(x>0).
①
(x)=3x2-(a+5),由于a∈[-2,0],从而当-1<x<0时,
(x)=3x2-(a+5)<3-a-5≤0,
所以函数f1(x)在区间(-1,0)内单调递减,
②
(x)=3x2-(a+3)x+a=(3x-a)(x-1),由于a∈[-2,0],所以0<x<1时,
(x)<0;
当x>1时,
(x)>0,即函数f2(x)在区间(0,1)内单调递减,在区间(1,∞)上单调递增.
综合①②及f1(0)=f2(0),可知:f(x)在区间(-1,1)内单调递减,在区间(1,+∞)内单调递增;
(II)证明:由(I)可知:f′(x)在区间(-∞,0)内单调递减,在区间(0,
)内单调递减,在区间(
,+∞)内单调递增.
因为曲线y=f(x)在点Pi(xi,f(xi))(i=1,2,3)处的切线相互平行,从而x1,x2,x3互不相等,且f′(x1)=f′(x2)=f′(x3).
不妨x1<0<x2<x3,由3
-(a+5)=3
-(a+3)x2=3
-(a+3)x3+a.
可得3
-3
-(a+3)(x2-x3)=0,解得x2+x3=
,从而0<x2<
<x3.
设g(x)=3x2-(a+3)x+a,则g(
)<g(x2)<g(0)=a.
由3
-(a+5)=g(x2)<a,解得-
<x1<0,
所以x1+x2+x3>-
+
,
设t=
,则a=
,
∵a∈[-2,0],∴t∈[
,
],
故x1+x2+x3>-t+
=
(t-1)2-
≥-
,
故x1+x2+x3>-
.
| a+3 |
| 2 |
①
| f | ′1 |
| f | ′1 |
所以函数f1(x)在区间(-1,0)内单调递减,
②
| f | ′2 |
| f | ′2 |
当x>1时,
| f | ′2 |
综合①②及f1(0)=f2(0),可知:f(x)在区间(-1,1)内单调递减,在区间(1,+∞)内单调递增;
(II)证明:由(I)可知:f′(x)在区间(-∞,0)内单调递减,在区间(0,
| a+3 |
| 6 |
| a+3 |
| 6 |
因为曲线y=f(x)在点Pi(xi,f(xi))(i=1,2,3)处的切线相互平行,从而x1,x2,x3互不相等,且f′(x1)=f′(x2)=f′(x3).
不妨x1<0<x2<x3,由3
| x | 21 |
| x | 22 |
| x | 23 |
可得3
| x | 22 |
| x | 23 |
| a+3 |
| 3 |
| a+3 |
| 6 |
设g(x)=3x2-(a+3)x+a,则g(
| a+3 |
| 6 |
由3
| x | 21 |
|
所以x1+x2+x3>-
|
| a+3 |
| 3 |
设t=
|
| 3t2-5 |
| 2 |
∵a∈[-2,0],∴t∈[
| ||
| 3 |
| ||
| 3 |
故x1+x2+x3>-t+
| 3t2+1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
故x1+x2+x3>-
| 1 |
| 3 |

练习册系列答案
相关题目
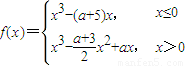
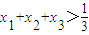 .
.