题目内容
设a∈[-2,0],已知函数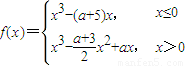
(Ⅰ) 证明f(x)在区间(-1,1)内单调递减,在区间(1,+∞)内单调递增;
(Ⅱ) 设曲线y=f(x)在点Pi(xi,f(xi))(i=1,2,3)处的切线相互平行,且x1x2x3≠0,证明
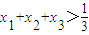 .
.
【答案】分析:(I)令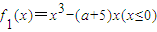 ,
,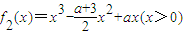 .分别求导即可得到其单调性;
.分别求导即可得到其单调性;
(II)由(I)可知:f′(x)在区间(-∞,0)内单调递减,在区间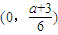 内单调递减,在区间
内单调递减,在区间 内单调递增.
内单调递增.
已知曲线y=f(x)在点Pi(xi,f(xi))(i=1,2,3)处的切线相互平行,可知x1,x2,x3互不相等,利用导数的几何意义可得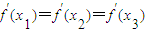 .
.
不妨x1<0<x2<x3,根据以上等式可得 ,从而
,从而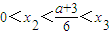 .设g(x)=3x2-(a+3)x+a,利用二次函数的单调性可得
.设g(x)=3x2-(a+3)x+a,利用二次函数的单调性可得 .
.
由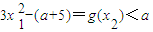 ,解得
,解得 ,于是可得
,于是可得 ,通过换元设t=
,通过换元设t=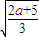 ,已知a∈[-2,0],可得
,已知a∈[-2,0],可得 ,
,
故
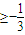 ,即可证明.
,即可证明.
解答:解:(I)令 ,
, .
.
① ,由于a∈[-2,0],从而当-1<x<0时,
,由于a∈[-2,0],从而当-1<x<0时,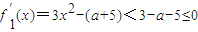 ,
,
所以函数f1(x)在区间(-1,0)内单调递减,
② =(3x-a)(x-1),由于a∈[-2,0],所以0<x<1时,
=(3x-a)(x-1),由于a∈[-2,0],所以0<x<1时, ;
;
当x>1时,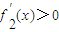 ,即函数f2(x)在区间(0,1)内单调递减,在区间(1,∞)上单调递增.
,即函数f2(x)在区间(0,1)内单调递减,在区间(1,∞)上单调递增.
综合①②及f1(0)=f2(0),可知:f(x)在区间(-1,1)内单调递减,在区间(1,+∞)内单调递增;
(II)证明:由(I)可知:f′(x)在区间(-∞,0)内单调递减,在区间 内单调递减,在区间
内单调递减,在区间 内单调递增.
内单调递增.
因为曲线y=f(x)在点Pi(xi,f(xi))(i=1,2,3)处的切线相互平行,从而x1,x2,x3互不相等,且 .
.
不妨x1<0<x2<x3,由 =
= .
.
可得 ,解得
,解得 ,从而
,从而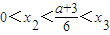 .
.
设g(x)=3x2-(a+3)x+a,则 .
.
由 ,解得
,解得 ,
,
所以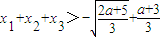 ,
,
设t=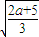 ,则
,则 ,
,
∵a∈[-2,0],∴ ,
,
故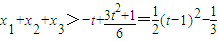
 ,
,
故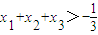 .
.
点评:本题主要考查了导数的运算与几何意义,利用导数研究函数的单调性,考查了分类讨论的思想、化归思想、函数思想,考查了分析问题和解决问题的能力.
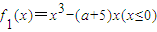 ,
,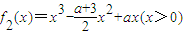 .分别求导即可得到其单调性;
.分别求导即可得到其单调性;(II)由(I)可知:f′(x)在区间(-∞,0)内单调递减,在区间
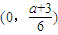 内单调递减,在区间
内单调递减,在区间 内单调递增.
内单调递增.已知曲线y=f(x)在点Pi(xi,f(xi))(i=1,2,3)处的切线相互平行,可知x1,x2,x3互不相等,利用导数的几何意义可得
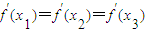 .
.不妨x1<0<x2<x3,根据以上等式可得
 ,从而
,从而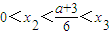 .设g(x)=3x2-(a+3)x+a,利用二次函数的单调性可得
.设g(x)=3x2-(a+3)x+a,利用二次函数的单调性可得 .
.由
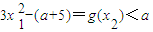 ,解得
,解得 ,于是可得
,于是可得 ,通过换元设t=
,通过换元设t=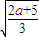 ,已知a∈[-2,0],可得
,已知a∈[-2,0],可得 ,
,故

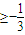 ,即可证明.
,即可证明.解答:解:(I)令
 ,
, .
.①
 ,由于a∈[-2,0],从而当-1<x<0时,
,由于a∈[-2,0],从而当-1<x<0时,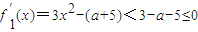 ,
,所以函数f1(x)在区间(-1,0)内单调递减,
②
 =(3x-a)(x-1),由于a∈[-2,0],所以0<x<1时,
=(3x-a)(x-1),由于a∈[-2,0],所以0<x<1时, ;
;当x>1时,
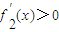 ,即函数f2(x)在区间(0,1)内单调递减,在区间(1,∞)上单调递增.
,即函数f2(x)在区间(0,1)内单调递减,在区间(1,∞)上单调递增.综合①②及f1(0)=f2(0),可知:f(x)在区间(-1,1)内单调递减,在区间(1,+∞)内单调递增;
(II)证明:由(I)可知:f′(x)在区间(-∞,0)内单调递减,在区间
 内单调递减,在区间
内单调递减,在区间 内单调递增.
内单调递增.因为曲线y=f(x)在点Pi(xi,f(xi))(i=1,2,3)处的切线相互平行,从而x1,x2,x3互不相等,且
 .
.不妨x1<0<x2<x3,由
 =
= .
.可得
 ,解得
,解得 ,从而
,从而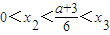 .
.设g(x)=3x2-(a+3)x+a,则
 .
.由
 ,解得
,解得 ,
,所以
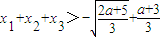 ,
,设t=
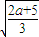 ,则
,则 ,
,∵a∈[-2,0],∴
 ,
,故
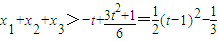
 ,
,故
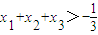 .
.点评:本题主要考查了导数的运算与几何意义,利用导数研究函数的单调性,考查了分类讨论的思想、化归思想、函数思想,考查了分析问题和解决问题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目