题目内容
对一切实数x,不等式x2+a|x|+1≥0恒成立,则实数a的取值范围是A.(-2,+∞) B.[-2,+∞)
C.[-3,+∞) D.(-3,+∞)
B ∵x2+a|x|+1=|x|2+a|x|+1≥0即a|x|≥-|x|2-1恒成立,
当|x|≠0时,a≥-|x|![]() .又-|x|
.又-|x|![]() ≤-2,当且仅当x=±1时取“=”.
≤-2,当且仅当x=±1时取“=”.
又x=0时,x2+a|x|+1≥0恒成立,∴当a≥-2时不等式恒成立.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
 在点A(x,
在点A(x, )处的切线斜率为k(x),且k (-1)=0.对一切实数x,不等式x
)处的切线斜率为k(x),且k (-1)=0.对一切实数x,不等式x k (x)
k (x) 恒成立(
恒成立(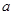 ≠0).
≠0). (1)的值;
(1)的值; >
>