Question

如图所示,已知四边形ABCD中,∠BAD=∠ABC=90°,PA⊥平面ABCD,PA=AD=3BC=3,AB=2.

(1)求点D到平面PAC的距离;

(2)若点M分的比为2∶1,求二面角M-CD-A的大小.

Answer 1

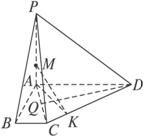
解法一：（1）过D作DQ⊥AC于Q.

∵PA⊥平面ABCD，

∴PA⊥DQ.

∴DQ⊥平面PAC.又由S_△ACD=AD·AB=AC·DQ，

AC=，∴DQ=.

∴D到平面PAC的距离为.

（2）过A作AK⊥DC于K点，连结MK.

∵PA⊥平面ABCD，∴MK⊥CD.

∴∠MKA为M-CD-A的平面角.

∵PA=AD=3,又=2，∴PM=2，MA=1.

在△ACD中，由面积相等，得AD·AB=CD·AK.

又CD=，∴AK=.

∴tan∠MKA==，

即二面角的大小为arctan.

解法二：以A为坐标原点，以所在直线为x、y、z轴建立坐标系.

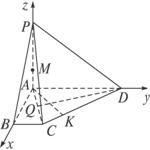
（1）过D作DQ⊥AC于Q，

∵PA⊥DQ,

∴DQ⊥平面PAC.

∴DQ就是D到平面PAC的距离.

设=m=m()=m(2,1,0),

∴=(0,-3,0)+m(2,1,0)=(2m,m-3,0).

由⊥，∴·=4m²+m(m-3)=0.

∴m=.

||==.

（2）过A作AK⊥DC于K，设= λ=λ(2,-2,0).

则=（2λ,3-2λ,0）.

∵⊥,∴·=0.∴λ=34.

∴||=.

∵MA⊥平面ABCD，∴MK⊥CD.

∴∠MKA就是M-CD-A的平面角.

∴tan∠MKA=.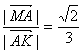

∴∠MKA=arctan.