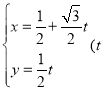题目内容
【题目】某商家计划投入10万元经销甲,乙两种商品,根据市场调查统计,当投资额为![]() 万元,经销甲,乙两种商品所获得的收益分别为
万元,经销甲,乙两种商品所获得的收益分别为![]() 万元与
万元与![]() 万元,其中
万元,其中![]() ,
,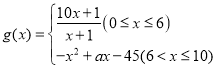 ,当该商家把10万元全部投入经销乙商品时,所获收益为5万元.
,当该商家把10万元全部投入经销乙商品时,所获收益为5万元.
(1)求实数a的值;
(2)若该商家把10万元投入经销甲,乙两种商品,请你帮他制订一个资金投入方案,使他能获得最大总收益,并求出最大总收益.
【答案】(1)![]() ;(2)投入甲商品的资金为
;(2)投入甲商品的资金为![]() 万元,投入乙商品的资金为
万元,投入乙商品的资金为![]() 万元,此时收益最大为
万元,此时收益最大为![]() 万元.
万元.
【解析】
(1)将![]() 代入
代入![]() ,即可求出
,即可求出![]() 的值;
的值;
(2)根据分段函数求出![]() 在
在![]() 和
和![]() 内的收益函数,分别利用基本不等式和二次函数求出两段的最值,然后比较大小即可得出结果.
内的收益函数,分别利用基本不等式和二次函数求出两段的最值,然后比较大小即可得出结果.
(1)依题意可得![]() ,解得
,解得![]() .
.
(2)设投入![]() 商品的资金为
商品的资金为![]() 万元
万元![]() ,则投入
,则投入![]() 商品的资金为
商品的资金为![]() 万元,
万元,
设收入为![]() 万元,则
万元,则![]()
①当![]() 时,
时,![]() ,
,![]() ,
,
则![]()
![]() ,当且仅当
,当且仅当![]() ,即
,即![]() 时,取等号.
时,取等号.
②当![]() 时,则
时,则![]() ,
,
因为![]() ,所以此时
,所以此时![]() ,
,
因为![]() ,所以最大收益为
,所以最大收益为![]() 万元,
万元,
答:投入甲商品的资金为8万元,投入乙商品的资金为2万元,此时收益最大,为17万元.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案【题目】某二手交易市场对某型号的二手汽车的使用年数x(0<x≤10)与销售价格y(单位:万元/辆)进行整理,得到如下的对应数据:
使用年数x | 2 | 4 | 6 | 8 | 10 |
销售价格y | 16 | 13 | 9.5 | 7 | 4.5 |
(1)试求y关于x的回归直线方程![]() .
.
(参考公式: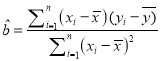 ,
,![]() )
)
(2)已知每辆该型号汽车的收购价格为ω=0.05x2﹣1.75x+17.2万元,根据(1)中所求的回归方程,预测x为何值时,销售一辆该型号汽车所获得的利润z最大?(利润=销售价格﹣收购价格)
【题目】![]() 年以来精准扶贫政策的落实,使我国扶贫工作有了新进展,贫困发生率由
年以来精准扶贫政策的落实,使我国扶贫工作有了新进展,贫困发生率由![]() 年底的
年底的![]() 下降到
下降到![]() 年底的
年底的![]() ,创造了人类减贫史上的的中国奇迹.“贫困发生率”是指低于贫困线的人口占全体人口的比例,
,创造了人类减贫史上的的中国奇迹.“贫困发生率”是指低于贫困线的人口占全体人口的比例,![]() 年至
年至![]() 年我国贫困发生率的数据如下表:
年我国贫困发生率的数据如下表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
贫困发生率 | 10.2 | 8.5 | 7.2 | 5.7 | 4.5 | 3.1 | 1.4 |
(1)从表中所给的![]() 个贫困发生率数据中任选两个,求两个都低于
个贫困发生率数据中任选两个,求两个都低于![]() 的概率;
的概率;
(2)设年份代码![]() ,利用线性回归方程,分析
,利用线性回归方程,分析![]() span>年至
span>年至![]() 年贫困发生率
年贫困发生率![]() 与年份代码
与年份代码![]() 的相关情况,并预测
的相关情况,并预测![]() 年贫困发生率.
年贫困发生率.
附:回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为:
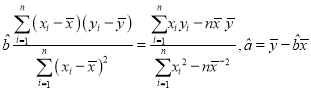 (
(![]() 的值保留到小数点后三位)
的值保留到小数点后三位)
【题目】为缓减人口老年化带来的问题,中国政府在2016年1月1日作出全国统一实施全面的“二孩”政策,生“二孩”是目前中国比较流行的元素![]() 某调查机构对某校学生做了一个是否同意父母生“二孩”抽样调查,该调查机构从该校随机抽查了100名不同性别的学生,调查统计他们是同意父母生“二孩”还是反对父母生“二孩”
某调查机构对某校学生做了一个是否同意父母生“二孩”抽样调查,该调查机构从该校随机抽查了100名不同性别的学生,调查统计他们是同意父母生“二孩”还是反对父母生“二孩”![]() 现已得知100人中同意父母生“二孩”占
现已得知100人中同意父母生“二孩”占![]() ,统计情况如表:
,统计情况如表:
性别属性 | 同意父母生“二孩” | 反对父母生“二孩” | 合计 |
男生 | 10 | ||
女生 | 30 | ||
合计 | 100 |
![]() 请补充完整上述列联表;
请补充完整上述列联表;
![]() 根据以上资料你是否有
根据以上资料你是否有![]() 把握,认为是否同意父母生“二孩”与性别有关?请说明理由.
把握,认为是否同意父母生“二孩”与性别有关?请说明理由.
参考公式与数据:![]() ,其中
,其中![]()
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|