题目内容
点M(x,y)在椭圆| 4x2 | 3 |
分析:要求x+y的最小值,因为点M(x,y)在椭圆
+4y2=1上,所以可考虑用椭圆的参数方程来求,可设x=
cosθ,则y=
sinθ,再利用辅助角公式,化一角一函数即可.再利用正弦函数的有界性来求最值.
| 4x2 |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
解答:解:∵M(x,y)在椭圆
+4y2=1上,可设x=
cosθ,则y=
sinθ
∴x+y=
cosθ+
sinθ=sin(θ+
)∈[-1,1]
∴x+y的最小值为-1
故答案为-1
| 4x2 |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
∴x+y=
| ||
| 2 |
| 1 |
| 2 |
| π |
| 3 |
∴x+y的最小值为-1
故答案为-1
点评:本题考查了利用椭圆的参数方程求最值的方法,做题适应认真观察,找到突破口.

练习册系列答案
相关题目
 =1上,则x+y的最小值为 .
=1上,则x+y的最小值为 .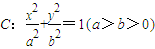 过点
过点 ,离心率
,离心率 ,若点M(x,y)在椭圆C上,则点
,若点M(x,y)在椭圆C上,则点 称为点M的一个“椭点”,直线l交椭圆C于A、B两点,若点A、B的“椭点”分别是P、Q,且以PQ为直径的圆经过坐标原点O.
称为点M的一个“椭点”,直线l交椭圆C于A、B两点,若点A、B的“椭点”分别是P、Q,且以PQ为直径的圆经过坐标原点O. 过点
过点 ,离心率
,离心率 ,若点M(x,y)在椭圆C上,则点
,若点M(x,y)在椭圆C上,则点 称为点M的一个“椭点”,直线l交椭圆C于A、B两点,若点A、B的“椭点”分别是P、Q,且以PQ为直径的圆经过坐标原点O.
称为点M的一个“椭点”,直线l交椭圆C于A、B两点,若点A、B的“椭点”分别是P、Q,且以PQ为直径的圆经过坐标原点O. 过点
过点 ,离心率
,离心率 ,若点M(x,y)在椭圆C上,则点
,若点M(x,y)在椭圆C上,则点 称为点M的一个“椭点”,直线l交椭圆C于A、B两点,若点A、B的“椭点”分别是P、Q,且以PQ为直径的圆经过坐标原点O.
称为点M的一个“椭点”,直线l交椭圆C于A、B两点,若点A、B的“椭点”分别是P、Q,且以PQ为直径的圆经过坐标原点O.