题目内容
已知 ,若函数
,若函数 的最小正周期是2,则f(1)= .
的最小正周期是2,则f(1)= .
【答案】分析:利用两个向量的数量积公式、两角和的正弦公式,可得f(x)=2sin( +ωx),根据周期的值求出ω,即得f(x)
+ωx),根据周期的值求出ω,即得f(x)
=2sin( +πx),则f(1)=2sin(
+πx),则f(1)=2sin( )=-2sin
)=-2sin ,运算求得结果.
,运算求得结果.
解答:解:由题意可得 =cosωx+
=cosωx+ sinωx=2sin(
sinωx=2sin( +ωx),故最小正周期是
+ωx),故最小正周期是 =2,
=2,
∴ω=π,故f(x)=2sin( +πx),则f(1)=2sin(
+πx),则f(1)=2sin( )=-2sin
)=-2sin =-1,
=-1,
故答案为:-1.
点评:本题考查两个向量的数量积公式的应用,两角和的正弦公式,正弦函数的周期性,求出f(x)=2sin( +πx),是解题的
+πx),是解题的
关键.
 +ωx),根据周期的值求出ω,即得f(x)
+ωx),根据周期的值求出ω,即得f(x) =2sin(
 +πx),则f(1)=2sin(
+πx),则f(1)=2sin( )=-2sin
)=-2sin ,运算求得结果.
,运算求得结果.解答:解:由题意可得
 =cosωx+
=cosωx+ sinωx=2sin(
sinωx=2sin( +ωx),故最小正周期是
+ωx),故最小正周期是 =2,
=2,∴ω=π,故f(x)=2sin(
 +πx),则f(1)=2sin(
+πx),则f(1)=2sin( )=-2sin
)=-2sin =-1,
=-1,故答案为:-1.
点评:本题考查两个向量的数量积公式的应用,两角和的正弦公式,正弦函数的周期性,求出f(x)=2sin(
 +πx),是解题的
+πx),是解题的关键.

练习册系列答案
相关题目


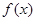 的最小正周期和值域;
的最小正周期和值域; 且
且 ,试判断△ABC的形状.
,试判断△ABC的形状. .
. ;
; ,求AB边上的高CD的长.
,求AB边上的高CD的长.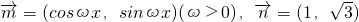 ,若函数
,若函数 的最小正周期是2,则f(1)=________.
的最小正周期是2,则f(1)=________. ,若函数
,若函数 的最小正周期是2,则f(1)=( )。
的最小正周期是2,则f(1)=( )。